浅海域での波浪特性として、浅海変形、屈折のため波高分布に空間的な差が生じる上、特に汀線近傍においては砕波による急激な波高減衰が生じることがわかっている。砕波に伴い汀線近傍の平均水位が上昇する現象をウェーブセットアップと呼ぶ。これは、波浪場が空間的に一様でない場合に、ラディエーション応力勾配に比例する平均的な外力が海水に作用して、これが平均水位の勾配と海浜流を引き起こし、結果として汀線付近の水位上昇をもたらすものである。

　この高潮にも影響を及ぼすWave Setupは、Longuet-HigginsとStewartによれば、次の定常な運動量方程式から求められる。

　

　

　ここで、Sxxはradiation応力、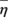は平均水位、hは水深であり、波はxの正方向に進行する。

　これを砕波帯内に適用し、砕波後の波高を、

　

　

とすると、海岸のWave Setup量は、

　

　

となる。ここでrは波高水深比、hbは砕波水深である。

　

　各層のradiation応力はLonguet-HiggingとStewartにならい、鉛直方向の分布式を層毎に積分することにより求められる。

　波はx軸に対して角度θで斜めに入射するとし、

　

　

と表す。ここで、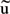はθ方向の波による水粒子の軌道速度、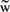は鉛直方向の水粒子速度である（図3-3-1参照）。

　

　

　静水面から深さzまでの鉛直断面を通過する過剰水平運動量束Sxx(Z)は

　

　

である。このSxx(z)を3つに分離し、

　

　

と表す。これらの式を積分すると、

　

　

となる。ここで、海水の密度をρ、重力加速度をgとすると、単位面積当たりの水面から水底までの水柱の持つ波エネルギーEは、波浪推算の諸元より、

　

　

で与えられる。またSyy(z)は、

　

　

となり、これをSxx(z)と同様に解くと、

　

　

となる。さらに、Sxy(z)は、

　

　

となる。

　いま、水深hをL層に分割し、第k層（k=1,2,・・・,L）のradiation応力を導く。ここで、第1層（表層）は海面z=ηからz=-h1、第k層はz=-hk-1からz=-hk、第L層（底層）はz=-hL-1からz=-hLとする（図3-3-2参照）。

　

　

　そして、各層における下記の量、

　

　

を導入する。

　これらを用いると、第k層まで積分したradiation応力は、

　

　

となる。

　ここで、第1層および第k層のradiation応力は、

　

　

　

となる。

　radiation応力の高潮数値モデルへの適用にあたっては、通常、

　

　

という形で組み込むことになる。

　

＜参考文献＞