Janssenのquasi-linear理論によれば、式（3-2-2-4）中の係数Bは次式で与えられる。

　

　

　ここに、ωは角周波数、ε=ρa/ρwでρaは大気の密度、ρwは海水の密度、パラメータβとxはそれぞれ次式で表される。

　

　

　

　ここに、βm、κはカルマン定数（=0.41）、U*は摩擦速度、cは位相速度、θは波向、ψは風向で、パラメータμは次式で表される。

　

　

ここに、

　

　

であり、z0は粗度長である。

　式（3-2-2-4）〜（3-2-2-9）で、摩擦速度U*と粗度長z0が与えられれば、Sinが求められる。WAMでは、U10を既知パラメーターとして、以下のようにして摩擦速度U*と粗度長z0が与えられる。

　海上風の風速分布は次の対数分布で表される。

　

　

　ここに、U（z）は高度zにおける風速である。また、粗度長z0は次式で与えられる。

　

　

　ここに、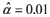、τは全応力（=ρaU²*）、τwは波による誘発応力で、次式で表される。

　

　

　波による誘発応力τwと全応力τとの比τw/τは、波齢の小さい波では約1で、波齢の大きい十分に発達した波では約0.5である。式（3-2-2-10）〜（3-2-2-12）は未知パラメータU*とz0に関して陰関数表示になっているが、方程式系は閉じている。したがって、z=10m、すなわち、U10を既知パラメータとして、式（3-2-2-10）〜（3-2-2-12）に適当な初期値を仮定し、逐次代入法を適用すれば、摩擦速度U*や粗度長z0を求めることができる。

　WAMでは、波浪推算に必要ないくつかのパラメータは事前に計算され、数値表に記憶される。波浪推算の本計算では、これらの数値表の値が内挿して用いられる。Sinの計算では、上記のように逐次代入法を適用する必要があることから、いくつかのパラメータは事前に計算され、数値表に記憶されて用いられている。

　

（3）エネルギー消散項Sdis

　初期の波浪推算モデルでは、風波のスペクトルが規定されたスペクトルまで発達するとスペクトルは飽和して、それ以上は発達しないと仮定することにより、便宜的にエネルギー消散が考慮されていた。WAMでは、以下に示すように直接的な表現でエネルギー消散項が考慮されている。

　WAMの消散項では、Hasselmann（1974）の白波理論に基づくKomen（1984）らの理論が採用された。この理論では高周波数領域で適切なエネルギーバランスを得るため、白波による消散項にκ²の項を加えることによって拡張されている。

　

　

　ここに、

　

　

　

　

　

であり、Cdis=4.5、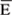は波浪スペクトルの全エネルギー、κは波数、＜ω＞および＜κ＞はそれぞれ平均角周波数および平均波数である。

　WAMでは、この他に、次式のようなJONSWAPの経験式（Hasselmann et al., 1973）に基づいた底面摩擦によるエネルギー消散項Sbfが定式化されている。

　

　

（4）非線形相互作用によるエネルギー輸送項Snl

　非線形相互作用によるエネルギー輸送は、波浪の非線形性によってスペクトルを構成する各成分波間でエネルギー輸送が行われる現象である。非線形相互作用によるエネルギー輸送の結果、各成分波のエネルギーは時間的に変化するが、成分波間でエネルギーが授受されるだけで、全エネルギーの積分値は変化しない。このため、スペクトルを積分して計算される有義波高などには直接には影響しない。しかし、実際にはエネルギー輸送によってスペクトル形が変化するため、これに伴って式（3-2-2-4）の風から波へのエネルギー輸送項や式（3-2-2-13）の砕波などによるエネルギー消散項も変化するため、間接的には全エネルギーにも影響が及ぶと考えられる。

　Hasselmann（1962）によると、非線形相互作用によるエネルギー輸送項Snlは次式で与えられる。

　

　

　ここに、n(k)=E(k)/ωは波の作用密度（Wave Action）で、積分核関数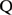はスペクトル成分の結合係数、δはデルタ関数を表す。デルタ関数は共鳴条件を表しており、以下の関係を満足する4つの成分波間で共鳴が生じる。

　

　

　ここに、kは波数ベクトル、ωは角周波数、添え字は4つの成分波を示す。図2-2-1-1はこの4つの成分波の関係を波数空間上に図示したものであり、同一直線状の4つの波数成分で共鳴が生じることを示している。

　ここに、成分波の進行方向をθとすると、k=(kcosθ,ksinθ)、k=｜k｜である。この図から、2つの成分波（3&4）が決まれば残りの2つの成分波（1&2）が1つの自由度γnl=const. の曲線上に決まることが分かる。ここに、γnlは次式で定義されるパラメータである。（Masuda, 1981）

　

　

　

　非線形相互作用によるエネルギー輸送項Snlは、式（3-2-2-5）の共鳴条件を満たす4つの成分波に対して式（3-2-2-4）を積分すれば良い。しかし、4つの成分波の組み合わせは無数に存在し、計算が非常に複雑である。このため、非線形効果を厳密な形で波浪推算モデルに組み込むことは現段階では困難である。

　そこで、WAMでは数多くの共鳴4波の組合せを用いて式（3-2-2-19）を数値積分する代わりに、図3-2-1の相互作用曲線の中心近傍のただ1つの共鳴4波の組み合わせを用いてSnlを近似したWAMで採用した共鳴4波の組合せは、パラメータλnlを用いて次式で表される。

　

　

　この組合せを用いれば、式（3-2-2-19）は次式のような簡単な形になる。

　

　

　ここに、Δω、Δω⁺、Δω^-は角周波数ω、ω⁺、ω^-の角周波数格子幅、δSnl、δSnl⁺、δSnl^-は方向スペクトルE、E⁺、E^-における非線形エネルギー輸送の単位時間あたりの変化量、Δθは波向の格子幅、Cnlは上記の近似法による結果が厳密計算値に合うように調節した無次元定数である。式（3-2-2-21）の左辺を全ての周波数および波向について足し合わせるとSnlが計算できる。なお、式（3-2-2-21）で表されるWAMの唯一の共鳴4波の組み合わせは、図3-2-1で上添字Wを付した濃い破線の矢印で示すものである。

　式（3-2-2-25）は、深海波を対象とした非線型相互作用の近似式であるが、浅海域では深海域に比べて非線型相互作用の影響は大きくなる。WAMでは、水深の影響を考慮した浅海波の計算を行う場合には、字式で表されるように、浅海波のための補正の尺度係数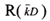を乗ずることによって浅海域の非線型相互作用を考慮している（WAMDI Group, 1988）。

　

　

　

　このように、無数の4波共鳴に伴う非線形エネルギー輸送をたった1組の組み合わせで代表させる近似法を、離散相互作用近似（Discrete Interaction Appro-ximation; DIA）と呼ぶ（S.Hasselmann and K.Hasselmann, 1985）。