|
3.1.2 河川内高潮モデル
(a)基本式
1次元の河川における高潮計算は、tを時間、水平軸xは下流に向けて正とすると、以下の運動方程式、連続式を数値的に解く方法を用いた。
ここに、Uは断面の平均流速、Qは断面の流量、Dは基準面からの水面の高さ、Rは径深、Bは川幅、ρは水の密度である。風のせん断力τsは海域の計算方法と同様な方法で与えた。海底摩擦力τbは宇野木ら(1999)の方法にならって、以下のように与えた。
ここに、αは1.0、粗度係数nは0.027を与えた。
河川内では気圧の効果は他項に比べ小さいので無視した。
(b)境界条件
(1)河川流量
河川流量は実測水位より求めた流量を河川上流地点に与えた。
(2)海域との境界
海域での水位、流量、流速を接続させた。
(3)水面の境界
海面の境界同様とした。
宇野木早苗・小西達男:河川感潮域の高潮計算における底面摩擦の評価、沿岸海洋研究第36巻、pp177-183(1999)
3.2.1 波浪推算の流れ
今回おこなった波浪推算におけるおおまかな流れを図3-2-1に示す。
・天気図データベースの作成
対象とした擾乱について、気象庁作成のアジア太平洋天気図(1日4枚:3時、9時、15時、21時)の気圧から等圧線データを読み取りデジタル化しデータベースとした。
・海上風の推算
作成した天気図データベースを入力とし、海上風の推算をおこなった。海上風の推算は、傾度風モデルを基本とし、マイヤーズの式を組み込んだハイブリッドモデルを用いた。なお、周防灘台風及び、仮想台風については、台風パラメータからマイヤーズの式により、海上風を推算した。
・波浪推算
海上風推算値を入力として、波浪推算をおこなった。用いた波浪推算モデルは、第3世代波浪推算モデルWAMである。
図3-2-1 波浪推算の流れ図
3.2.2 波浪推算手法
本研究における波浪推算法は、第3世代波浪推算モデルであるWAMを使用した。この波浪浪推算法は、発達期の風波成分と減衰期のうねり成分を考慮可能な波浪推算法であり、波の発達と減衰、非線型相互作用などを同時に考慮可能である。
以下に、K.HasselmannやG.J.Komenらが中心となって組織したWAMDIグループが開発したWAMについて概説する(WAMDI Group,1998、Komen et al.,1994)。
(a)波浪推算モデルの概要
(1)基礎方程式(エネルギー平衡方程式)
WAMでは、直交座標系と球面座標系の2つ基礎方程式が用意されている。深海条件で流れのない場合を考えると、球面座標系で表した基礎方程式は次式で表される。
ここに、
であり、φ、λおよびθはそれぞれ緯度、経度および波向、Rは地球の半径、C gは群速度、gは重力加速度、ωは角周波数( 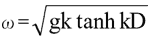 )、kは波数、Dは水深である。 WAMでは、式(3-2-2-1)の右辺のエネルギーソース関数に、次の3つの項が考慮されている。
WAMの特徴は非線形相互作用によるエネルギー輸送項Snlを直接的に考慮している点にある。
(2)風から波へのエネルギー輸送項Sin
風から波へのエネルギー輸送項Sinは一般にSin=A+B・Eと表現されることが多い。ここに、AはPhillipsの共鳴機構(Phillips,1957)に関するもので、波浪スペクトルの線形的な発達を示す。B・Eは、風から波への支配的なエネルギー機構であるMiles機構(Miles,1957)に関するもの、波浪スペクトルの指数関数的な発達を示す。WAMの最新バージョンであるCycle4ではPhillipsの共鳴機構に関するAの項を無視し、次式を用いている。
このため、初期状態で波浪スペクトルのエネルギーが0であれば、そこでは波が発生しないので注意が必要である。
また、Cycle4では、従来用いられていた入力項に代え、新たにJanssen(1989,1991)のquasi-linear理論を導入した。この理論の採用により、同じ風場が与えられた場合でも海面の状態に依存して風から波へのエネルギー輸送量が異なることになり、より現実に近い定式化に改良された。すなわち、波齢の大きな波よりも波齢の小さな波の方が、風から波へのエネルギー輸送が活発に行われる。
|