|
(2)RLの直列回路
図7・26
図7・26は、コイルの自己インダクタンスL〔H〕には僅かの抵抗R〔Ω〕があるので、これを想定した回路である。
これを等価回路ともいう。
この合成抵抗を求めるには、抵抗R〔Ω〕の部分は電圧と電流が7・4・2(1)で述べたように同相であるが、自己のインダクタンスL〔H〕の部分では電圧が
電流よりπ/2進んでいる。
このように位相が異っているところではそれぞれ別々に計算し、次にそれらをベクトル的に合成することが計算上便利である。
この場合、流れる電流をi= 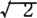 Isinωt〔A〕とすればRの両端に加わる電圧は
| (拡大画面:73KB) |
 |
上式中の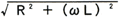 は、この回路において、交流電流を妨げる抵抗RとリアクタンスωLとを合成したもので、これをインピーダンスと称し、Zの量記号で表し、その単位にはオーム(単位記号Ω)を用いる。 は、この回路において、交流電流を妨げる抵抗RとリアクタンスωLとを合成したもので、これをインピーダンスと称し、Zの量記号で表し、その単位にはオーム(単位記号Ω)を用いる。
したがって、(7・3・8)式は次のようになる
説明 “インピーダンスについて”
2πfL=ωL、1/2πfC=1/ωCはそれぞれ誘導リアクタンス、容量リアクタンスと称し、XL、Xcの量記号で表し、その単位にはオーム(単位記号Ω)を用いることは前述のとおりである。これらを単にリアクタンスと称しXで表することもある。
ところでインピーダンスとは、これらに抵抗Rを加えた、一種の電流を妨げる抵抗であって、これにはベクトルインピーダンスとインピーダンスとがある。前者はZ、後者はZの量記号で表し、単位にはいずれもオーム(単位記号Ω)を用いる。
その一例として、RとXとが直列回路の場合のインピーダンスは次のように表す。
|