|
11. 開口隅部の応力集中
11.1 応力集中係数
小型船、型船、特に漁船では機関室開口や魚倉の大型ハッチの隅部等の応力の集中し易い箇所への配慮が十分でないように見受けられる。平均応力レベルが低い時は損傷に至らぬかもしれないが、予期せぬ波浪衝撃等により致命的損傷を招く恐れがあるので、十分な配慮、が必要である。
開口隅部での最大応力は開口隅部のr止まりから15〜30°内側に入った点に生じ、その応力集中係数は、主として隅部の半径rと開口巾bとの比により決まる。
応力集注係数 K=σmax/σ0
隅部の形状が円弧状の場合の応力集中係数の計算式を下図に示す。隅部形状が楕円形状の場合はこれより係数は小さくなる。
11.2 応力集中と構造様式の関係
1)隅部の二重張り又は厚板挿入は応力集中係数値の減少に殆ど効果はない。
2)倉口縁材の形状寸法も応力集中には余り影響しない。
3)隅部の形状寸法は応力集中に最も敏感に影響を与える。
11.3 実船実績値
| 船種 |
GT(トン) |
b(mm) |
r(mm) |
b/r |
k |
| 帆立養殖 |
14 |
1,700 |
150 |
11.33 |
2.35 |
| 小型底曳 |
9.7 |
1,750 |
50 |
35.00 |
4.12 |
| 延縄 |
9.7 |
1,700 |
50 |
34.00 |
4.05 |
| 遊漁 |
19 |
2,500 |
100 |
25.00 |
3.37 |
| 定置網 |
19 |
2,000 |
100 |
20.00 |
3.00 |
| 採介藻 |
4.9 |
1,400 |
50 |
28.00 |
3.60 |
| 沖合底曳 |
29 |
1,900 |
150 |
12.66 |
2.45 |
| 旅客 |
23 |
3,400 |
100 |
34.00 |
4.05 |
|
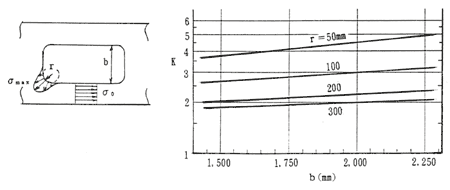
K値は極力3以下に押さえたい。下図にb、rによるK値の変化を示す。
甲板口周辺の応力集中
応力集中係数K=1.5+0.075b/r
但し0.025<r/b<0.25
| (拡大画面:16KB) |
 |
12. シューピースで支持される舵の舵頭材とシューピースの寸法の決め方
アルミニウム合金製漁船構造基準(案)では吊下げ舵のみを規定し、シューピース支持形式の舵は時間切れのため未制定となっている。然し基本的考え方の大筋は既に審議されているので、この考え方は十分実設計の参考となし得る。
(基本的な考え方−図12−1 参照)
●吊下げ舵の舵頭材の径を計算の基準とする。
●舵はシューピースで80%支持とする。
●シューピース支持の舵頭材の径は、吊下げ舵形式とシューピース支持形式の船体の、転舵時のサイドスリップの差(吊下げ舵形式の方が大きい)を考慮に入れなければ、
| シューピースが100%支持の場合 |
吊下げ舵の径の63% |
| シューピースが80%支持の場合 |
吊下げ舵の径の74% |
|
となる。
●然し実際にはシューピース支持形式の方がサイドスリップは小さいため、吊下げ舵形式より舵板に働く直圧力は大きくなるから、舵頭材の径はそれに対応する修正力泌要。
●以上の考察により、舵頭材の径の要求最終値についての審議は未了ではあるが、その径は最大でも吊下げ舵の80%とすれば十分とみなされる。
●舵頭材の径が決まればシューピース支持80%に見合うシューピース断面の寸法が次式から求められる。
|
I/IR×lR3/l3=12
∴I=12×IR×(l/lR)3
|
|
|
となり、これに適合するシューピース断面の寸法(深さ、巾、板厚さ)を決めればよい。
(計算式の説明−次頁図参照)
シューピースと舵は相持ち構造と考えると、転舵時に舵先端にシューピースの反力Rが働く。その時の舵先端及びシューピースの撓みをそれぞれδR、δSとすれば、δR=δSであるから、
1/ERIR(P0cosθ/8−R/3)lR3=R/3EI3・・・(1)
となる。θ=35○とすれば(1)式は
1/ERIR(0.819P0/8−R/3)lR3=R/3EI3・・・(2)
シューピースのない時の舵先端の撓みをδ1とすれば、
δ1=P0cosθ・lR3/8ERIR=0.819P0・lR3/8ERIR・・・(3)
ここでδR=αδ1とすれば、(2)及び(3)式より
R/P0=0.307(1−α)・・・(4)
さらにER=3E(SUS又はSSとA5083)とすれば、結局
I/IR×12R3/l3=(3/α−3)・・・(5)
となる。
従って、これら(4)及び(5)式より次のことが判る。
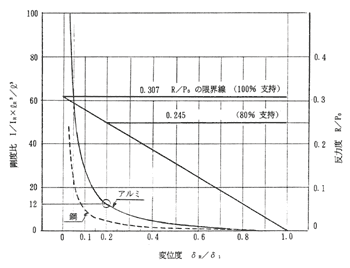
1)α=0ではシューピースは100%支持となり、その時のシューピースの反力R=0.307P0が反力としての限界値(最大値)となる。
2)α≦0.2となると(5)式により1/IR×lR3/l3の値は急激に増加する。従ってシューピースに余り厳しい支持条件を求めるのは得策ではない。
3)以上よりα=0.2を採用することにすれば、(5)式より
1/IR×lR3/l3=12
∴I=12×IR×l3/lR3・・・(6)
となる。
図12−1 シューピース支持型舵におけるシューピースの変位度、反力度及び剛度比の関係
記号
IR:舵頭材の断面二次モーメント
I:シューピースの断面二次モーメント
lR:舵の深さ(船底〜かじ下端)
l:シューピースの長さ
ER:舵頭材のヤング率
E:シューピースのヤング率
w:舵板に働く等分布荷重 P0:舵板に働く直圧力
θ:舵角
R:相持ち構造のシューピースにかかる反力
δ1:シューピースのない時の舵先端の撓み
δR:相持ち構造の舵先端の撓み
δS:反力Rによるシューピースの撓み
剛度比:I/IR×lR3/l3
反力度:R/P0
変位度:δR/δ1
δR=1/ERIR(P0cosθ/8−R/3)lR3
δS=Rl3/3EI
| (拡大画面:26KB) |
 |
13 甲板及び船底外板の座屈応力の計算
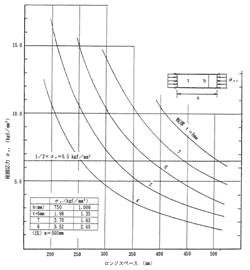
船体の曲げモーメントにより圧縮荷重を受ける甲板や船底外板に対しては、座屈応力に留意しなければならない。通常デザインの縦構造方式の場合は殆ど問題はないが、薄板を使用する場合や縦横のの骨間隔が比較的広い横構造方式の場合、或いは甲板開口部等については座屈応力をチェックする必要がある。その計算式、及びトランススペースを500mmとした場合の代表的な板厚とロンジスペースによる座屈応力を図13−1 に示す。船体縦強度計算での許容曲げ応力値は1/2σyを基準としているから、座屈応力もこれ以上となることを基準とする。
相対する2辺に一様な圧縮荷重を受ける長方形板の座屈応力σcrは
σcr=KE(t/b)2(kgf/mm2)
茲にt:板厚(mm)
a:荷重を受けない辺の長さ=長辺の長さ =トランスのスペース(mm)
b:荷重を受ける辺の長さ=短辺の長さ=ロンジのスペース(mm)
E:ヤング係数
K:係数。茲では4辺支持の矩形板とする。
Kはa/b>1の領域で波状に変化するが、ここではK=3.62(一定)とする。
図13−1 |
トランススペースa=500mmとした場合の板厚〜ロンジスペース〜座屈応力 |
| (拡大画面:34KB) |
 |
|