|
4. 材料の強度と破壊
4.1 応力とひずみ
1)垂直応力
長さL、断面積Aの棒の上端を天井に固定し(補・40図(a))、下端に下向きの力を加える。棒は引張られて伸びると同時に内部に内力を発生して外力に抵抗する。外力を増加して行くと伸びも増加し、遂には棒の材料が抵抗しきれなくなって断面が破断する。このような現象を追いながら材料力学に現れる述語を定義しよう。まず、力がP(kgf)になったとき棒の長さがL’になったとする。下端で下向きの力Pを受けている棒は、上端で天井をPの力で下方に引張っている。作用・反作用の法則より棒は天井からPの力で上方へ引張られている。したがって、棒全体に外から作用する合力はゼロとなり、釣り合いが保たれている(補・40図(b))。任意の断面ABより下の部分に注目する。もし、この断面を通して、上の部分がこの部分に何の力も及ぼしてないとすると、ニュートンの運動方程式P=mαに従ってこの部分は加速度αで下の方へ飛んでいってしまう。ここでmは考えている部分の質量である。したがって、の部分が静止しているためには、断面ABを通して上の部分がこの部分をPの力で上向きに引張っていなければならない。これで注目している部分に外から働く合力がゼロになり、釣り合いが取れることになる(補・40図(c))。もちろん、さらに任意の断面CDを考えても、ABCDの部分には釣り合いが取れていなければならない(補・40図(d))。このように、棒のどの部分をとっても、その部分の境界面を通して外から働く力は釣り合いの式を満足しなければならない。棒の任意の断面(断面積A)における単位面積当たりの力σを応力といい、次式で定義される。
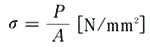 ・・・(1) A:棒の任意の断面における断面積(mm2)
この応力は考える断面に垂直に作用しているから垂直応力と呼ばれる。また、単位長さ当たりの伸びεをひずみといい次式で定義される。
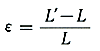 ・・・(2)
補・40図 軸方向の引張り荷重をうける棒の応力
2)応力・ひずみ線図
板状あるいは丸棒の標準試験片を材料試験機にかけて引張り、荷重と伸びを計測することにより、材料の力学的性質が求められる。試験片にかかる力Pの増加と共にそれが伸びてゆく有り様は、横軸にひずみ、縦軸に応力をとった応力・ひずみ線図で表される(補・41図)。応力とひずみは点Aまでは比例する。この範囲を弾性域という。この範囲では、荷重を取り去ると、もと来た道をたどり荷重ゼロで変形も消えて元の状態に帰る。点Aにおける応力σYを降伏応力という。これ以上にさらに荷重を増すとひずみは急速に増加し両者の比例関係は成立しなくなる。点Cに至って棒は破断する。このときの応力σBを抗張力あるいは引張り強さという。降伏応力を越えた任意の点Bで荷重を取り去ると応力・ひずみ関係はもときた道を逆にたどらず、弾性域の直線に平行に下降し、荷重ゼロでB1に達する。B点におけるひずみεのうちB11B2に当たる弾性ひずみεeは回復し、OB1に当たる塑性ひずみεPは荷重を完全に取り去っても永久に残るひずみである。この状態から再び荷重をかけるとB1からBまで弾性範囲となるが、これは降伏応力が大きくなったことに相当する。この現象を加工硬化という。
補・41図 延性材料の応力・ひずみ線図
3)せん断応力
断面積Aの鋲継ぎ手に両側から力Pがかかるとき(補・42(a))、鋲の横断面には板がすべろうとするのを妨げる抵抗力が働く(補・42図(b))。次式で定義される単位面積当たりの値τをせん断応力という。
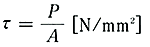 ・・・(3)
これは考える面に平行に働く力である。長さh隔たった平行な面がeだけずれたときの相対的なずれの量、すなわち、単位長さ隔たった平行な面のずれの量γをせん断ひずみといい次式で定義される(補・42図(c))。
補・42図 鋲継手のせん断応力
(a)
(b)
(c)
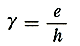 ・・・(4)
ある面にせん断応力が存在すると、その面に直交する面上に、大きさが同じで、方向については、力のベクトルの矢の矢頭あるいは矢尻同士が向かい合うようなせん断応力が存在するという特性がある。すなわち、せん断応力は単独では存在せず、必ずそれに直交するせん断応力を伴う。
4)フックの法則
棒を引張ったときの垂直応力と伸びひずみ、および、鋲継ぎ手におけるせん断応力とせん断ひずみの間の関係は、弾性域内では共に比例関係にある。これがフックの法則で、それぞれ、次のような関係式で与えられる。
σ=Eε[N/mm2]・・・(5)
τ=Gγ[N/mm2]・・・(6)
E[N/mm2]をヤング率あるいは縦弾性係数、G[N/mm2]を剛性率あるいは横弾性係数という。これらは、材料に固有の材料定数である。棒を引張れば、軸方向に伸びるが横方向には縮む。この横方向の圧縮ひずみεtと縦方向の引張りひずみεとの比νはポアソン比と呼ばれ、次式で定義されるが、これも材料定数である。
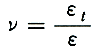 ・・・(7)
等方性材料では、独立な材料定数は以上の3個である。
5)モールの応力円
物体内の応力は、その働く面の位置と方向が与えられて初めて大きさと方向が決まる。一般には、力の方向は面に対して傾いているので、ベクトル的に分解して、垂直応力とせん断応力に分けて考える。せん断応力が存在しない面に働く垂直応力を主応力といい、その面を主応力面という。主応力面は互いに直交しており、主応力は考える点における最大および最小の垂直応力である。最大せん断応力は主応力面と45度をなす面で生じる。
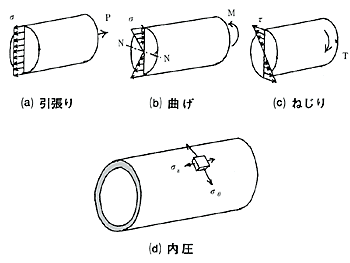
直径dの棒を力Pで引張ったとき、M[N/mm2]の曲げモーメントで曲げたとき、あるいは、T[N/mm2]の捩りモーメントで捩ったときに棒の横断面に生ずる応力の分布を、それぞれ、補・43図に示す。 引張ったときには断面全体に次式で与えられる一様な引張り応力σが生ずる(補・43図(a))。
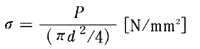 ・・・(8)
曲げたときには、中立軸からの距離に比例して、へこんだ側は圧縮の、出張った側は引張りの垂直応力が分布する(補・43図(b))。中立軸は中心を通る曲げモーメントの軸NNで、伸びも縮みもしない。最大の曲げ応力σmaxは(曲げモーメント)/(断面係数)で与えられるが、円形断面に対しては、次のようになる。
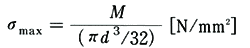 ・・・(9)
断面が、幅b[mm]、高さh[mm]の長方形の場合には、次式で最大曲げ応力が与えられる。
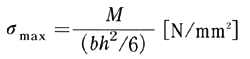 ・・・(10)
捩ったときには、断面全体にわたって、中心からの距離に比例し、円周の接線方向に向いたせん断応力が生ずる(補・43図(c))。最大のせん断応力τmaxは次式で与えられる。
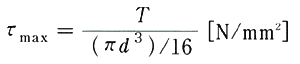 ・・・(11)
これらの図には、代表的な直径に沿う応力分布を示した。内径d[mm]、厚さt[mm]で内圧P[N/mm2]を受ける薄肉円筒の圧力容器に生ずる応力は、平面応力あるいは2次元応力と呼ばれる(補・43図(d))。フープ応力あるいは円周方向応力σθおよび軸応力σz、は、それぞれ、以下の式で与えられる。
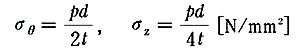 ・・・(12)
これらの応力分布はすべて外力と応力の釣り合い式より求められる。
補・43図 種々の負荷により生ずる応力
| (拡大画面:20KB) |
 |
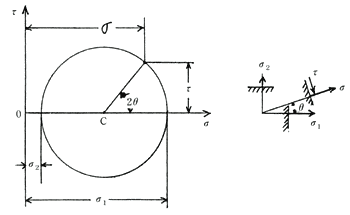
物体内のある点における任意の面とその面上の応力との関係はモールの応力円によって与えられる。これは横軸に垂直応力を、縦軸にせん断応力をとり、最大主応力σ1と最小主応力σ2を与える横軸上の2点を通る線を直径とする円である(補・44図)。いま考えている面の法線と最大主応力面の法線のなす角度θの2倍の角度2θを、円の中心Cにおいて、横軸に対してとった半径とモールの円との交点Pの横座標および縦座標が、それぞれ、その面上の垂直応力σとせん断応力τを与える。また、それらの値は、次式で与えられる。
 ・・・(13)
これらの関係式は、考える面および2つの主応力面に平行な三角形要素の釣り合いより求められる。
補44図 モールの応力円
| (拡大画面:12KB) |
 |
|