|
3.3 危険速度
最近になり、舶用機関に高速機関が広く用いられ始めている。それに伴い、機関につながる軸系の回転数も次第に高速化して来た。同じ動力を伝える場合、回転数が高ければそれに逆比例して伝達回転力は小さくなり、したがって軸はそれだけ細くなる。この様な場合に考慮しなければならない現象が最近舶用の軸系でも問題になって来ている。
この現象について述べよう。
補・39図に示すように比較的細い一様な軸の中央に質量Mの円板が乗っている。このMをハンマで叩いたとするとこの系はMを集中荷重、軸の曲げ剛性を復元力とする横振動をすることはすぐに想像できる。ただ一般にこの振動は振動数が高く、直接目で見ることは難しい。しかし軸にストレンゲージを貼りつけて観測すれば簡単にオシログラフの画面で振動を見ることができる。この図のような単純な軸系であればその固有振動数は簡単に
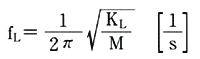 ・・・(14)
ともとまる。KLは材料力学でよく知られているビームの式から
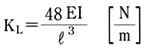 ・・・(15)
と求めることが出来る。ただし、Eは鋼の縦弾性係数、Iは軸の断面2次モーメントである。今この軸をnc≡60fL[min−1]で回転させるとすると軸はすさまじいふれまわりを始め、たちまち大きく曲がり、破壊する。そこでここで定義した横振動数に対応する回転数nc[min−1]をふれまわりの危険速度Critical Speedという。実際問題として軸はn=0. 8nc[min−1]でもふれまわりが激しく、とても定常的な運転をすることはできない。したがって機械は軸系の回転速度n[min−1]が
0.75nc<n<1.25nc・・・(16)
の範囲では連続運転をしない事になっている。
舶用の機関の場合、主軸系のフランジを現場や工場で不用意に重いものに変えたり、またねじり強度の上からは十分の強さがあるからという理由で主軸系の一部や機関付属の機器類の軸を細くするなどのことを行うと、この危険速度の影響でふれまわりが大きくなる場合を生じる。横振動も正確にいえばどの軸系もいくつかの固有振動数が存在するから当然それぞれに対応する危険速度が存在する。しかし多くの場合は最も低い横振動数に対応する危険速度のみが問題となる。この現象で注意しなければならないのは、この現象は力学的不安定現象であり、振動に減衰を与えれば防止できるとか、危険速度でのふれまわりを小さくおさえることは本質的に不可能である。軸にのっている、質量を減ずる、ベアリング間隔を短くする、軸の曲げ剛性を大きくする、すなわち軸を太くするなどの系の振動特性を代えてfLの値、したがってncの値を変更する以外にこの現象から逃れる方法はないことである。
なお、数値例として、l=1,800mm、M=5.Okg、軸径d=30mmの場合を考えると、I=3.97×104mm4となるから、E=2.06×105N/mm2を用いると、K=67.4N/mmであり、P=1161/s
すなわちnc=1109rpm
となる。
補・39図 単純な系の横振動
|