6.4 曲げモーメントに対する安全性の検討
(1) 曲げモーメントが作用する部材は、次式を満足しなければならない。
(6.4.1)
| ここに、 |
γi : |
|
構造物係数 |
| |
Md : |
|
設計曲げモーメント |
| |
Mud : |
|
設計曲げ耐力 |
(2) 設計曲げ耐力Mudは、次式により計算する。
Mud=M(fd)/γb
(6.4.2)
| M(fd) : |
|
材料の設計強度fdに対する曲げ耐力 |
| γb : |
|
材料係数 |
曲げ耐力M(fd)の計算は、以下の仮定に基づいて求めてよい。
a) コンクリートの引張応力を無視し、維ひずみは断面の中立軸からの距離に比例する。
b) コンクリートの応力―ひずみ曲線は、図−5.2による。
c) 鋼材の応力―ひずみ曲線は、正曲げで鋼板に引張応力が生じる場合は、図−5.1による。負曲げで鋼板に圧縮応力が生じる場合は、次式により、圧縮鋼板圧を鋼板の座屈を考慮した等価厚さに換算する。
(6.4.3)
| ここに、 |
teq : |
|
圧縮鋼板の等価厚さ |
| |
t'f : |
|
圧縮鋼板の厚さ |
| |
b : |
|
部材軸方向に配置された補剛材の間隔(スタッド間隔) |
| |
Es : |
|
圧縮鋼板のヤング係数 |
| |
f'yd : |
|
圧縮鋼板の設計圧縮降伏強度 |
| |
| |
|
|
f'yd=fyk/γs |
| |
| |
fyk : |
|
鋼材の圧縮降伏強度の特性値 |
| |
γs : |
|
材料係数 |
d) 部材断面のひずみがすべて圧縮となる場合以外は、コンクリートの圧縮応力度の分布を図−6.1に示す長方形圧縮応力度の分布(等価応力ブロック)と仮定してよい。
k1=0.85
図−6.1等価応力ブロック
【解説】
(1)について 合成版の曲げ耐力M(fd)は鋼板を、正曲げに対しては引張鉄筋、負曲げに対しては圧縮鉄筋とみなし複鉄筋断面として計算を行えばよいことが、多数の実験によって確認されているので、本文ではRC方式によることとした。
(2)について 補剛された鋼板は局部座屈後も残留強度があり、曲げモーメントおよび軸方向力に対する終局限界状態時にもその寄与が期待できる。既往の研究によれば、部材軸方向に配置された補剛材がコンクリート内に十分に埋め込まれ、引き抜きが起こらなく、補剛材による鋼板の拘束効果が十分に期待できる場合、補剛材間の鋼板の設計圧縮強度は、以下の式で安全側に推定できることが知られている。したがって、負曲げによって鋼板に圧縮応力が生じる場合は、局部座屈を考慮して設計曲げ耐力を算定することとした。
圧縮鋼板の取り扱いについて
圧縮鋼板の応力―ひずみ曲線は、鋼板の座屈を考慮した次式によって求められる。
σ's=Esε's(ε's≦f'ud)
(6.4.4)
σ's=f'ud(σ's≦f'ud)
(6.4.5)
ここに、
(6.4.6)
| σ's : |
|
圧縮鋼板の圧縮応力度 |
| Es : |
|
圧縮鋼板のヤング係数 |
| ε's : |
|
圧縮鋼板の圧縮ひずみ |
| t'f : |
|
圧縮鋼板の厚さ |
| b=a |
(格子配列:2辺固定2辺自由版) |
| b=(4.0/6.74)・a |
(千鳥配列:2辺固定2辺単純支持版) |
| b : |
|
圧縮鋼板の部材軸方向に配置された補剛材の間隔(図解−6.3参照) |
| a : |
|
スタッドの間隔に基づく正方形座屈モデルの一辺の長さ。 |
| k : |
|
座屈係数。スタッドの座屈抑止効果、配列による拘束条件を確認した。 |
| |
|
実験結果に基づき、座屈係数は、以下のとおりとする。 |
| 千鳥配列の場合k=6.74(2辺固定2辺単純支持版) |
| 格子配列の場合k=4.00(2辺固定2辺自由版) |
ここでは、上記のf'udを用い、等価厚さteqを次のように求める。
(6.4.7)
図解−6.3 スタッドの配列とa値
6.5 せん断力に対する安全性の検討
(1) せん断力に対する安全性の検討は、棒部材、面部材等の部材の種類、せん断力の作用方向を考慮して適切に行わなければならない。
(2) 俸部材においては、棒部材の設計せん断耐力Vydおよび腹部コンクリートの設計斜め圧縮破壊耐力Vwcdに関して安全性の検討を行う。
(3) 面部材が面外力を受ける場合には、荷重状態(分布荷重、集中荷重)や部位に応じて適切に面外せん断力に対する安全性の検討を行う。
(4) せん断力に対する安全性の検討は次式により行う。
(6.5.1)
| ここに、 |
γi : |
|
構造物係数 |
| |
Vd : |
|
設計せん断力 |
| |
Vud : |
|
設計せん断耐力で、Vvd、Vwcdいずれか小さい方の値とする。 |
(5) 設計せん断耐力Vydは、式(6.5.2)によって求めてよい。
Vyd=Vcd+Vsd
(6.5.2)
| ここに、 |
Vcd : |
|
せん断補強鉄筋を用いない棒部材の設計せん断耐力で、式(6.5.3)による。 |
Vcd=η3・βd・βp・βn・fvcd・bw・d/γb
(6.5.3)
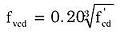 |
(N/mm2) |
ただし、fvcd≦0.72N/mm2 |
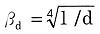 |
(d:m) |
ただし、βd>1.5となる場合は、1.5とする。 |
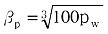 |
|
ただし、βp>1.5となる場合は、1.5とする。 |
| βn=1+Mo/Md |
(N'd≧0の場合) |
ただし、βn>2となる場合は2とする。 |
| =1+2Mo/Md |
(N'd<0の場合) |
ただし、βn<0となる場合は0とする。 |
| N'd : |
|
設計軸方向圧縮力(圧縮を正) |
| Md : |
|
設計曲げモーメント |
| M : |
|
設計曲げモーメントMdに対する引張縁において、軸方向力によって発生する応力を打ち消すのに必要な曲げモーメント |
| bw : |
|
腹部の幅 |
| d : |
|
有効高 |
Pw=As/(bw・d)
| As : |
|
引張鋼材の断面積 |
| f'cd : |
|
コンクリートの設計圧縮強度(N/mm2) |
| η3 : |
|
低減係数(ρ/2300)3/2 *1 |
| γb : |
|
部材係数 |
| Vsd : |
|
せん断補強鉄筋により受け持たれる設計せん断耐力で、式(6.5.4)による。 |
| ρ : |
|
使用する超軽量コンクリートの単位容積質量(kg/m3) |
*1「平成12年度 高性能軽量コンクリートを用いた港湾構造物検討調査 報告書(国土交通省 北陸地方整備局 新潟港湾空港技術調査事務所)」
Vsd=[Awfwyd(sin αs+cos αs)/ss]z/γb
(6.5.4)
| Aw : |
|
区間Ssにおけるせん断補強鉄筋の総断面積 |
| fwyd : |
|
せん断補強鉄筋の設計降伏強度 |
| αs : |
|
せん断補強鉄筋が部材軸となす角 |
| ss : |
|
せん断補強鉄筋の配置間隔 |
| z : |
|
圧縮応力の合力の作用位置から引張鋼材図心までの距離で一般にd/1.15としてよい。 |
(6) 腹部コンクリートのせん断に対する設計斜め圧縮破壊耐力Vwcdは、式(6.5.5)によって求めてよい。
Vwcd=fwcd・bw・d/γb
(6.5.5)
| ここに、 |
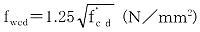 |
ただし、 |
fwcd≦7.8N/mm2 |
【解説】
(3)について 設計せん断耐力の算定式(6.5.2)は、集中荷重をうける棒部材を対象とし、比較的スレンダーなはりの斜めひび割れ耐力に基づいて規定されたものである。
このため、支点付近の区間のせん断耐力や、分布荷重をうける擁壁、ボックスカルバート等の面部材について、せん断補強鉄筋を配置することを前提としたはり部材に関する支持部付近の設計法をそのまま適用することは合理的でないことが指摘されている。したがって、本マニュアルでは、面部材については、荷重状態、部位に応じて、適切な方法で面外せん断に対する安全性の検討を行うものとし、具体的には、以下の方法で設計してよい。
外壁、底版のような3辺固定版や4辺固定版においては、曲げモーメント分布形状の違いがせん断耐力に影響を与える。このため、曲げモーメントが零になる点(反曲点)を境に2本の斜めせん断ひび割れが発生する実験事実等に基づいて、支点から反曲点までと、反曲点から最大曲げモーメント点までをそれぞれの区間の等価せん断スパンとして耐力を棒部材あるいはディープビーム式により算定し、各区間の耐力を定め、弱い区間の耐力をその部材の耐力とする方法(図解−6.4参照)により検討する。
ただし、
h/2≦x1≦1.5d
h/2≦x2≦1.5d
x1、x2それぞれ等価せん断スパンa1、a2の中央で、h/2を下回る場合はh/2、1.5dを超える場合は1.5dとする。
図解−6.4 せん断耐力算定において設定するせん断スパンと検討断面の位置
a) 検討断面の位置は、それぞれ等価せん断スパン中央で、h/2(h:部材高さ)を下回る場合はh/2、1.5d(d:有効高さ)を超える場合は1.5dとする。
b) 設計せん断耐力Vcdは、コンクリート標準示方書に示される以下のディープビーム式により求めてよい。
Vdd=βd・βp・βa・fdd・bw・d/γb
(6.5.6)
ここに、Vdd:ディープビームの設計せん断耐力
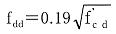 |
(N/mm2) |
|
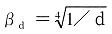 |
(d:m) |
ただし、βd>1.5となる場合は、1.5とする。 |
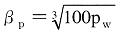 |
|
ただし、βp>1.5となる場合は、1.5とする。 |
 |
|
|
| av : |
|
せん断スパン |
| d : |
|
荷重作用点における有効高さ |
| pw : |
|
軸方向引っ張り鉄筋断面積の腹部断面積に対する比率 |
| f'cd : |
|
コンクリートの設計圧縮強度(N/mm2) |
| bw : |
|
腹部の幅 |
| γb : |
|
部材係数 |
なお、式(6.5.6)は、1/h(1:はりスパン、h:部材高さ)が5程度(せん断スパン比a/dが2.5程度)で通常の集中荷重を受けるはり部材のせん断耐力式にすりつき、かつ1/hが2程度(せん断スパン比a/dが1程度)以下の範囲において実験結果と適合するように、安全側に簡略化してディープビーム式として定められたものである。また、現在のところ、ディープビームでは、せん断補強鉄筋の効果については、実験により確認されているものの、定量化されるに至っていなので、式(6.5.6)では、せん断補強筋の効果を考慮していない。