4.3 凝結過程
従来のモデルの場合は、水蒸気量が飽和水蒸気量を超えた時に、雲を発生させる。
したがって完全に飽和して全天が雲に覆われているか雲が全く存在しないかのどち
らかになり、連続的でない雲の分布をつくり、現実的ではない。また、サブグリッ
ドの雲を無視するため、常に過小評価になってしまう。また、潜熱などの発生が急
激なので、雲の初期には特に影響を及ぼす。
そこで、準保存的(quasi-conservative)な量
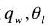
を使い、統計的方法によって部分
凝結を考慮したモデルを取り入れ、サブグリッドの雲・霧を表すことを可能にして
いる。
部分凝結を考慮したモデル
Sommeria and Deardorff(1977),Mellor(1977)に従って
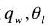
は正規分布を取ると仮定
する。
雲の格子点体積にしめる割合
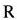
は下記で定義される。
この式を簡単化すると雲の格子点体積にしめる割合
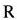
と雲水量
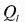
は、
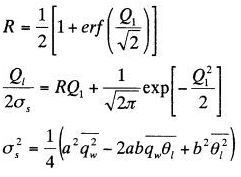
ここで、乱流クロージャーモデルレベル2.5の仮定と、勾配拡散近似から、
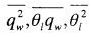
は、代数的に求めることができる。
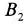 |
: 乱流クロージャ一定数(10.1) |
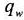 |
: 総水分量(total water specific humidity) |
 |
: 水の温位(liquid water potential temperature) |
また、その他の関数は、以下であらわされる。
Sommeria and Deardorff(1977)によると、このモデルには以下のメリットがある。
・雲水量や
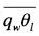
のフラックスが増加する。
またその分布は、より高い高度まで達することができる。
・雲内の層で

の振動が小さくなる。