2.3 夏季における気温の年々変動の長期傾向*
*内田洋平(日本気象協会関西支社海洋調査課)
2.3.1 はじめに
第1章で述べたように、最近では地球温暖化の影響として年々変動の激化(冷害/猛暑、旱魃/多雨が頻繁に発生すること)が示唆されている。しかしながら統計的な有意性を考慮した解析は少ない。ここでは冷害の頻度の長期変化を統計的に検証するために、夏(6〜8月)の日最高気温の年々変動における統計的な傾向を山元ら(2001)と同じ方法で調査する。
2.3.2 方法
調査地点として、日本の気象官署のうち1899〜1999年の101年間で日最高気温の欠測が2回以下の地点を検索した。選出された58地点は前章で選んだ地点と一部異なっている。欠測期間の値は前後の年から内挿した。気温の調査は平均気温で行うことが多いが、この調査では日最高気温を対象にした。日最高気温は1日1回最高最低温度計で観測することが可能なので、1日数回以上の観測が必要な日平均気温算出の際のあいまいさを回避できる。
(拡大画面: 51 KB)
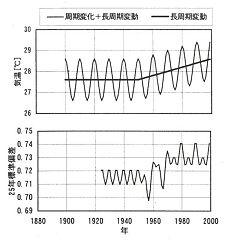
図2.3.1移動標準偏差とトレンドの関係
山元の方法では25年標準偏差を年々変動の指標とするが、このとき長周期変動(トレンド)があると正しく評価できない。この問題の例として、単調に増減する短い周期のサインカーブに途中から単調増加するトレンドを加えたものと、その25年標準偏差を移動平均的に求めたものを、図2.3.1に示す。図に示すように、年々変動はかわらないのに単調増加のトレンドにより標準偏差も増加してしまっている。
本調査では短周期変動成分を抽出するため、以下に述べるDFT(離散フーリエ変換)によるハイパスフィルターを用いた。
まずDFTを適用して長周期の変動を得るために、次のようにデータの長さを2倍した。100年間の時系列x(i),(i=1,2,....,100)に同じデータを折り返し追加して200年の時系列y(j)を得る。
このデータからDFTによりフーリエ級数を求める。
ここにAk,Bkはそれぞれ余弦・正弦の係数である。このときk=1,2,..,8の係数はそれぞれ200,100,66.7,50,40,33.3,28.6,25年の周期における振幅を示しているので、これらを合成した値は元の変動における25年以上の周期からなる成分となる。
もとの時系列からこの時系列を差し引いた値は25年以上の周期のトレンドが消去されている。
解析には短周期成分を100年間の平均値と標準偏差により標準化したデータを使用する。
2.3.3 全国的な年々変動の傾向
全国的な傾向を見るために気象官署58地点のデータを平均した夏の日最高気温の変動を求めた。全国平均した夏の日最高気温、その周期別成分、前25年間のデータから移動平均的に求めた標準偏差の経年変化を図2.3.2に示す。
(拡大画面: 37 KB)
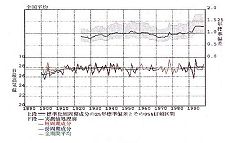
図2.3.2 全国平均した夏の日最高気温の年々変動
図の25年標準偏差で示される年々変動は、1930年頃までは小さかったが1950年代までに極大を迎え、その後1970年代に極小となる。また近年の25年間では大きく増加している。
これらの変化が統計的に有意かどうか見るために、1900〜1999年を25年毎の4期間に分け、期間同士で分散が異なるかどうか検定する等分散検定(F検定)を行った。
F検定は分散の比F=(snew)2/(sold)2が自由度[nnew-1,nold-1]の F-分布における信頼区間内にあるかどうかで分散が等しいか検定する。ここにsnew(sold)は最近(過去)の25年標本標準偏差、nnew(nold)はデータ数である。本調査では分散の増減に注目しているので常に最近/過去となるように分子分母を選択する。nnew=nold=25なのでこの分散比Fは自由度[24,24]のF-分布に従い、F≧1.98(≦O.51)のときに有意水準5%で近年になって年々変動が大きく(小さく)なっていると結論できる。
期間相互間のF検定の結果を表2.3.1に示す。表によると1975〜1999年の分散は1900〜1924年および1950〜1974年のものより有意水準5%で大きいので、最近25年間の年々変動は激しくなっていると結論できる。
表2.3.1 全国平均した夏季平均日最高気温の25年毎の分散比
有意水準5%で有意に増加しているケースにハッチをかけた
| 分母\分子 |
1925〜1948 |
1950〜1974 |
1975〜1999 |
| 1900〜1924 |
1.323 |
0.955 |
2.148 |
| 1925〜1948 |
− |
0.722 |
1.624 |
| 1950〜1974 |
− |
− |
2.250 |
一般に温度環境は地域によって異なると考えられるため、ある地点の変動が別の地点の変動を打ち消してしまう可能性がある。そこで観測地点毎に求めた分散の頻度分布を期間毎に求めた。図2.3.3に分散の期別頻度分布を示す。図では1975〜1999年の分散が他の期間より増加している地点が明らかに多くなっている。ただし全ての地点で増加しているかどうかはわからないので地点毎に年々変動の変化傾向を調査する。
2.3.4 分散比の地理的分布
以下では1900〜1999年を4つに分けて、それぞれの期間を1期(1900〜1924)、2期(1925〜1949)、3期(1950〜1974)、4期(1975〜1999)と呼ぶ。観測地点毎に4つの期間同士でF検定を行い結果の地理的分布を調査した。図2.3.4に地図上にプロットしたF検定の結果を示す。
1期から2期にかけて北海道、東関東、太平洋岸を除く西日本で、有意ではないが年々変動が増加傾向にある(図2-3-4(a))。2期から3期では西日本を除いて有意ではないが減少傾向にある(図2-3-4(b))。3期から4期では関東甲信越〜西日本において有意に増加傾向にあった(図2-3-4(c))。それ以外の地域でも有意ではないが増加傾向にあった。
最近25年間で以前より有意に年々の変動性が増加しているのは関東から西日本までの地域である。
(拡大画面: 71 KB)
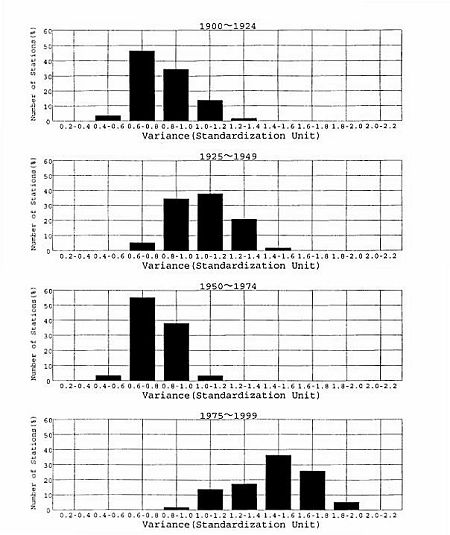
図2.3.3 夏季平均日最高気温の25年分散の期間別頻度分布
2.3.5 標準偏差時系列のクラスター解析
25年標準偏差時系列で階層的クラスター解析を行った。
クラスター解析では、各時系列のデータ同士の類似度を算出し、類似度が近いもの同士を順にグループ化していく。類似度およびグループ化する方法は幾つかある(例えば田中ら1983)。この調査では類似度としてユークリッド距離、クラスター構成法として群平均法を採用した。
解析の結果を示す樹形図とできたグループごとに印を付けた地図を図2.3.5に示す。ここではひとつの目安として6つのグループに分けた。
これらの図から地域分けを試みると、北日本日本海岸(旭川、網走、札幌、寿都、函館、青森、秋田、新潟)、北日本太平洋岸(根室、帯広、宮古、石巻、福島)、北九州(下関、福岡、佐賀、長崎、熊本)といったグループができる。しかし{長野、横浜、浜松、津、宮崎、松山}といった同一地域とは言い難いグループも形成されている。また西日本では幾つかのグループがバラバラに分布していて地域的分類とは言い難い。