2.2.4 有意なトレンドの検出
ここでは、前節の地域区分に基づき、各地域の降水変化量の特徴を示し、その長期変化傾向(トレンド)の有意性を評価した。
図2.2.7に各地域の降水変化量の時系列を示す。データは標準偏差により規格化している。EOF第1モードの結果が示すように、北海道以外の地域において、1940年前後または199O年代の降水変化量が大きい傾向にある。また、地域、年代よっては、降水変化量に数十年スケールのトレンドがあるように見える。
(拡大画面: 148 KB)
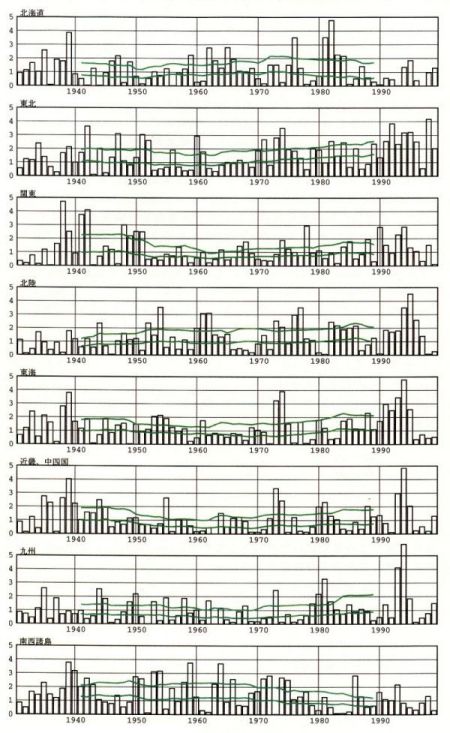
図2.2.7 各地域における降水変化量の経年変化 値は標準偏差により規格化している。図中の緑色のラインは21年移動平均値の95%信頼区間を示す。
次に、各地域の降水変化量のトレンドの有意性を評価する。ここでは、降水変化量に対して40年〜60年の10年毎のトレンドテストを実施した。手法は以下に概説するThe Man-Kendal testを用いた。
The Man-Kendal testは仮説検定により時系列に対して有意なトレンドを検出する手法の一つである。今、時系列をyt(t=1,…,N)とする。各値yt'(t’=1,…,N-1)とyt(t=t’+1,t’+2,…,N)の大小を比較し、以下に従って新たな時系列Zkを作成する。
ここに、k=((t’−1)(2N-t’)/2)+(t-t’)。The Man-Kendal statistic Sは以下のようにZkの合計によって表される。
Sは時系列のすべての組み合わせについて、その差が正の値になる数から負の値になる数を引いた値を示している。test statistic ucはN>40の条件の下で、以下のように示される。
ここで、nはytとyt'が同値になったグループの数、eiはi番目のグループのデータ数を示す。S=0の場合、ucは0と仮定される。統計量ucは標準正規分布に従い、仮に、有意水準をαとしたときにlucl>u1−α/2となる場合には、「時系列は上昇または下降トレンドである」という仮説を否定できない。なお、Kendal(1975)は、同値グループが少ないときにはNが10程度の場合にもこのテストは有効であると述べている。しかし、Nが小さい場合には、必然的にトレンドテストの結果の信頼性が乏しいと考えられる。また、このトレンドテストはトレンドの大小に関わらずその有意性を評価する。したがって、量的に有意な増減を評価する手法ではないことを留意する必要がある。
以上の手法によって、トレンドテストを実施した結果を図2.2.8に示す。図2.2.8のグラフは、当年を含む前n年間(n=40,50,60)のデータにより計算されたucの時系列を示している。ここでは、有意水準αを5%とし、uc〉1.96の場合には、n年間の降水変化量に有意な上昇トレンド、ucく−1.96の場合には有意な下降トレンドが存在すると判断する。
以下、各地域のトレンドの特徴を述べる。
降水変化量のトレンド
| 北海道 |
:有意な変化傾向は検出されない。 |
| 東北 |
:1930年代半ばから現在にかけて有意な増加傾向 |
| 関東 |
:1950年代半ばから1990年代半ばに有意な増加傾向 |
| 北陸 |
:有意な変化傾向は検出されない。 |
| 東海 |
:1930年代前半から1970年代前半に有意な減少傾向 |
| |
:1950年代後半から1990年代後半に有意な増加傾向 |
| 近畿、中四国 |
:1930年代半ばから1980年代に有意な減少傾向 |
| |
:1950年代半ばから1990年代半ばに有意な増加傾向 |
| 九州 |
:1950年代半ばから1990年代半ばに有意な増加傾向 |
| 南西諸島 |
:1930年代初めから現在まで有意な減少傾向 |
上記のトレンドの特徴だけを見ると、例えば、東海では1930年代前半から1970年代前半に有意な減少傾向、1950年代後半から1990年代後半に有意な増加傾向とあり、減少傾向と増加傾向が重なる期間が存在し、一見すると矛盾する用に思えるが、ここではそれぞれの期間に限定したトレンドテストの結果を示しているので、減少傾向の期間の後半と増加傾向の期間の前半が重なることもあり得る。
以上より、ここで定義した東北、関東、東海の各地域においては少なくとも1950年代から現在にかけて降水変化量が増加傾向にあると判断される。また、北海道と南西諸島の降水変化量に関しては、本州の降水変化量の変動とは明らかに異なる特徴を持っていると思われる。北海道では、本州の上記3地域の変化に対し、1950年代から現在にかけて降水変化量の増減は検出されない。また南西諸島に関しては、名瀬と石垣島の2点のみからの評価となるので、再検討が必要かも知れないが、ここでの結果では、近年は降水変化量が減少傾向と判断される。
(拡大画面: 98 KB)
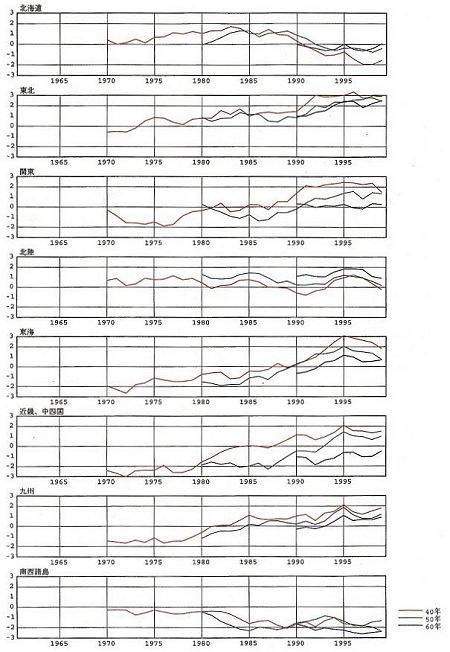
図2.2.8 各地域における降水変化量に関するトレンドテストの結果 図中の各ラインは、当年を含む前n年間(n=40,50,60)のデータにより計算されたucの時系列を示している。ucは、Mann-Kendall test(本文参照)によって算出される統計量であり、正規分布に従う。ここでは、有意水準αを5%とし、uc〉1.96の場合には、n年間の降水変化量に有意な上昇トレンド、ucく−1.96の場合には有意な下降トレンドが存在すると判断する。