ここでzはライザーの縦方向の位置(海底を0とし、上向きを正とする)で、d_n (z)はn番目の固有関数である。変数q_n (t)はn次モードの瞬時値(質量係数、モード関与係数、一般化座標)を示す。Y方向の変位に関しても同様の式が存在する。ライザーの傾き、すなわち、垂直線からの角度は、式(2)をzについて微分することによって求められる。これにより、

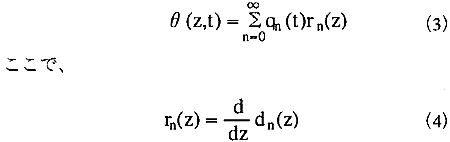
は、d_n (z)における回転の固有関数である。

X方向のライザーの真の変位量を評価する方法は以下の通りである。z₁, z₂, z₃, z₄, z₅, z₆を、ライザーに取りつけられた測定装置容器の位置とし、これらの座標値を式(2)と式(3)に代入して測定装置の位置での変位量と角度を求める。これを行列式で表現するため、以下の各行列を定義する。

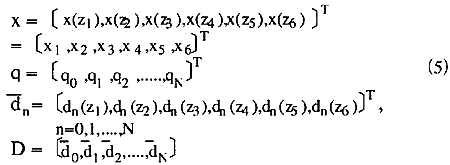
ここで、N次より高次のモードは応答に影響しないものと仮定する。モード質量と任意の座標値における変位量の関数は、以下のようになる。

x=Dq　(6)

同様に、モードから角度への関数も、以下のように記述できる。

θ=Rq　(7)

ここでθとRはxとDの場合と同様の類推で定義している。

加速度計の信号ベクトルをa=[a₁, a₂, a₃, a₄, a₅, a₆]^Tと定義すると、これらの測定値に関するモデルは、以下のようになる(参照：式1)。

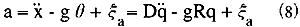
ここで、ξ_aは測定ノイズのベクトルで、式を完成させるのに必要な項である。ここで言うノイズとは、物理的ノイズや外乱という意味に限定せず、一般的なセンサーの欠陥や誤差など、あらゆる種類の測定誤差の原因を含むものとする。

次に、3、4、6の測定位置における回転速度センサーの信号をρ₁, ρ₂, ρ₃とすると、回転速度に関する以下の式が得られる。

前ページ　　　目次へ　　　次ページ