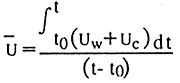方向の異なる波と海流
元のFerrari & Bearmanモデルには、波と海流が共直線性を持たない状態には対応していない。通常、海流は波から独立しているので、設計の検証用に採用するデータには、波と海流の方向が違っているケースがあるのが一般的である。このような場合には、図2のフローチャートに示す手順を使用する。フローチャートから、以下の3つの場合が予測される。
(i) 波と海流の角度αが小さい(例えば45°、今後実験にて検証する)場合、共直線性を仮定した元の式(1)および式(2)を使用する。
(ii) 角度差αが(i)で示した限度より大きく、波による流速と海流による流速の比が小さい(例えば0.5<Uw/Uc<2.0、今後実験にて検証する)場合、両者の影響が相殺し、渦励振は発生しないと仮定する。
(iii) 角度差αが(i)で示した限度を超え、なおかつ、波による流速と海流による流速の比が(ii)で示した限度を超える場合、波と海流のうち影響の大きいものだけを考慮して、小さいものは無視する。影響の大きい方の作用について、式(1)と式(2)を使用する。
不規則波の解析:
より精度の高い解析結果が求められる場合には、不規則波の解析を行なう。元のモデルには不規則波解析は含まれていないが、組込みは簡単に行える。不規則波解析の組込みは、次式の累積平均速度を定義する積分計算に基づいて、渦のはく離の平均周波数を求める。
ここでは、規則波の解析のように分析的な方法は取らない。積分の時間範囲(t-to)は、波が誘起する流速のゼロ交差によって定義する。