Fw=fA-Zu-H_upP　(3)

ここでAは、時間平均した水平自由水面上に選択した参照点すなわち原点(x,y) = (0,0)における、障害を受けない入射波の増分の振幅である。「励起力係数」列ベクトルf、2乗「放射インピーダンス」[3,8]行列Z、およびN_u×N_p行列H_upは、線形システムに関する周波数依存の複素変換関数を表す。

入射波および放射波による振動水柱内部の水の体積流量(m³/s)は、以下に示すN_p次元の列ベクトルで表される。

Q_w=qA-Yp-H_puu　(4)

ここで、「励起体積流量係数」列ベクトルq、2×2「放射アドミタンス」[6]行列Y、およびN_p×N_u行列H_puは、線形システムに関する周波数依存の複素変換関数を表す。ここで、放射インピーダンスと放射アドミタンスの行列は対称であることに注意する。

Z^T=Z and Y^T=Y　(5)

これは、流体力学ポテンシャル理論によって導出される[5,7]。

これらの方程式を、以下の行列式にまとめて記述する。

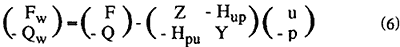
この式は、図1のブロック線図で表される線形システムに相当する。この式の右辺第1項は、入射波と放射波の組合せによる励起量である。励起力と励起体積流量を組合せて以下の励起ベクトルを定義する。

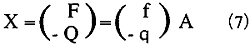
ここで、回折問題が振幅uおよびpがゼロの振動に相当することに注意を要する。式(6)の最終項は、振幅uおよびpによる放射問題に相当する。この項は、以下のようにも記述できる。

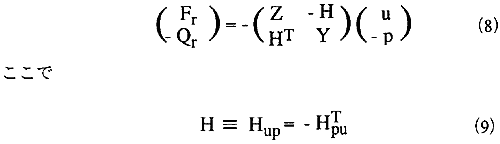
(上添え字Tは転置行列を示す)。この反対称(後の式)が正しいことは、流体力学ポテンシャル理論[5,7]を適用することによって示される可能性がある。また、このことは以下からも示される。式(8)がF_rとpについて解かれるとすると、これらはuとQ_rを使った対称N×N行列で表される。これは、pとQ_rがそれぞれ振動水柱における力と速度の測定値であることによる。

前ページ　　　目次へ　　　次ページ