13.　将来の年間インフレ率をiとすると、n年度半期の名目的支払い額1ポンドは、次のような実質的額(0年度の通貨価値による)となる。

　

　

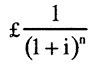
実質割引率をrとすると、この支払い額の0年度における現価は、次式から得られる。

　

　

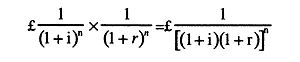
(1+i)(1+r)-1=i+r+irは、実質割引率rに対応する「名目」割引率である。多くの場合、特にインフレ率が低いと、名目割引率としてi+rを使用するだけで十分である。こうした近似計算を行い、インフレ率に整数を採用する場合は、表1-3の係数を使用できる。

　

(i)　将来5年間のインフレ率を年平均4パーセントと予測する。5年度の半期に名目的支払い額100ポンドを1回で支払う必要がある。0年度半期の一般物価レベルによる0年度半期におけるその現価は、割引率6+4=10パーセントを使用し、表2から概算できる。したがって、その概算現価は£100×0.6209=£62.1となる。さらに精確な割引率は((1.04×1.06)-1=0.1024となるので)10.24パーセントになる。この割引率を使用すると、その現価は次のように算定される。

　

　

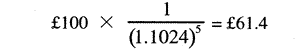
(ii)　将来6年間のインフレ率を年平均4パーセントと予測する。各年半期に所定の名目的支払い額50ポンドを支払う必要がある。この一連の支払い額に対する(0年度半期の一般物価レベルによる0年度半期における)現価は、割引率10パーセントと表3を使用して概算できる。その概算現価は£50×O.4355=£217.8となる。

　

さらに精確な割引率は((1.04×1.06)-1=0.1024となるので)10.24パーセントになる。この割引率を使用すると、上記支払い額の現価は、公式(3)により次のように算定できる。

　

　

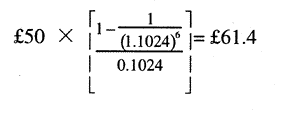
相対価格の変動

14.　時には事前評価において、特定の商品やサービスに対する相対価格の変動、つまり一般物価レベルに対比した変動を考慮に入れる必要もある。商品やサービスの価格が「総合インフレ率に対比して年間一定率jで」上昇すると仮定すれば、この相対価格変動の所定値を割引率の計算に組み込むことができる。そうした「調整ずみ」割引率は[(1+r)/(1+j)]-1=(r-j)(1+j)となる。特にjが小さい場合には、r-jを使用する近似計算でも十分精確な値が得られることも多い。

前ページ　　　目次へ　　　次ページ