状態量としての流速、圧力、温度、濃度はそれぞれ時間平均値Ui（i=1，2，3）、P、Θ、Cと変動成分ui（i=1，2，3）、p、θ、cの和で表す。ここでは直交デカルト座標xi（i=1,2,3; x3は鉛直方向）をとり、時間をtとする。また、以下に示す諸式はテンソル表示とし、添字については総和規約に従うものとする。

　解析対象は空気であり、その密度をρ1とし、ヒュームの密度をρ2、濃度はC（0≦C≦1）である。ρ0は代表密度でρ0=ρ1とする。

　平均流速Ui、平均温度Θおよび平均濃度Cに関する状態方程式は以下のように表される。

　

　

　ただし、vは動粘性係数、κ=v/Prは熱拡散係数、Prはプラントル数、λ=v/Scは物質拡散係数、ScはSchmidt数、gは重力加速度、ρは密度、βは数体積膨張係数、Θ0は場の平均温度、qt（Wm^-3）は発熱量、qc（s^-1）はガスの発生速度、δijはクロネッカーのデルタである。

　ζはβに倣って作ったで、濃度変化による浮力である。密度ρ=Cρ2+（1-C）ρ1とすると、

　

　

が得られる。ここに、Δρ=ρ2-ρ1

　標準的な渦拡散モデルでは、レイノルズ応力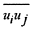、乱流熱流束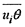および乱流物質流束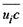は次の式で表される。

　

　

　ここに、kは乱流エネルギー（k=uiuj/2）、vtは運動量の乱流拡散係数（渦動粘性係数）ktは熱の乱流拡散係数、λtは濃度の乱流拡散係数である。

　

　乱流エネルギーの散逸率をεとすると、渦動粘性係数はvt=Cμk²/ε、（Cμ=0.09）により求められる。ここで、kとεに関する輸送方程式は次のように表される。

　

　

　ここに、式中の普遍常数はLaunder等の実験により求められた、σk=1.0、σε=1.3、Cε1=1.44、Cε2=1.92、cε3=0.7を用いる。

　温度場と濃度場に対しては、0方程式モデルを使用して、乱流熱拡散係数κt及び乱流濃度拡散係数λtは以下のように計算する。

　

　

　ここに、Prtは乱流プラントル数、Sctは乱流Shmidt数であり、Prt=1.0、Sct=1.0を用いる。

　

　壁面の付着境界層では壁法則を用い、粘性低層および対数領域に分けて次式で表す。

　

　

　ここに、Utは壁に接線方向の流速、Kはカルマン定数（=0.42）、E=9.7である。また、y⁺は壁座標（=yur/V）、uτは摩擦速度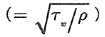である。さらに、τwは壁面からのせん断応力であり、

　

　

で表される。

　この場合の乱流エネルギーとその散逸率は次のようになる。

　

　

　ただし実際の計算では壁に一番近い格子点が粘性低層（y⁺＜10）の中にある場合にはk=0を用いる。

　壁面における熱的境界条件は温度Θwまたは熱流束qwを与えるものとする。

　

　

　ここにnは壁に垂直方向であり、断熱壁ではqw=0となる。

　ガス濃度の境界条件は次式で表される。

　

　

　計算には有限体積法を応用したSIMPLE（Semi-Implicit Method for Pressure-Linked Equation）法を用いる。