|
3.3 モード3におけるLPV制御系設計
(定格出力に維持するための最適回転数制御)
モード3における制御目的は、発電機の過負荷を防ぐために、風力発電機の出力P=QAωを定格出力Pratedに維持することであるので、獲得する風エネルギーと定格出力の間に、次のような関係
が満足される必要がある。ゆえに、動作点の周速比は出力係数CPの逆関数を用いて、次のように求められる。
(18)式の出力係数の逆関数は、Fig. 5に示すように、最適周速比(λ=λopt)以外では解を2個持つ多価関数である。これは、ロータの回転数を上げる、または回転数を下げて運転することによって、定格出力を維持することが可能であることを意味する。安全性の面から後者の方法を採用すると、(18)式は一意に表わされる。(18)式を利用し、風速Vに対する最適回転数ω*は
と表される。ゆえに、制御目的は次のように表される。
モード3においてはモード2とは異なり、動作点の周速比λ*は(18)式に従い変動するために、(12)式の係数Ap(V)の偏微分項dCT/dλも風速Vに応じて複雑に変動する。ゆえに、係数が風速に対してFig. 7のように変動するために、線形補間モデルを導出することができない。
そこで本論文では1つの解決策として、Fig. 8に示すように、空力特性(トルク係数)曲線を2次関数近似する。
Fig. 7 Relationship between 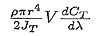 and wind speed in mode 3 and wind speed in mode 3
|
| Fig. 8 |
Approxmated torque coefficient CT Curve of Wind Lens |
(21)式を(8)式に代入して線形化すると、次に示すような風速Vと回転数ωの2つの変数をスケジューリングパラメータに持つ線形補間モデルが導出される。
ただし、
モード3においては、風速Vと最適回転数ω*(19)式に従い、Fig. 9に示すような関係で表されるので、本論文では、それを包含するような三角形領域を選択し、その端点Ak,(k=1,2,3)を用いて線形補間タイプのLPVモデルを導出する。
ただし、
ここで得られた、線形補間タイプのLPVモデルから拡大系を構成し、Ak,(k=1,2,3)のぞれぞれ端点での数学モデルに対してLMIを導出する。そして、モード2と同様にしてγを最小化する準最適化問題として解くことによりLPVコントローラを設計する。
Fig. 9 LPV system variation in mode 3
|