はじめに、（8）式の非線形方程式を動作点周りで一次近似することにより線形状態方程式を導出するため、動作点について確認する。動作点は静的な釣り合い状態であるので、

　

　

となる。右肩添字の^*は動作点における値を意味する。よって、動作点における制御入力i^*は

　

　

と表される。また、動作点における周速比λ^*を用いて、風速Vに応じた回転数ω^*は（6）式より、

　

　

と表される。

　次に（8）式は、風速が一定の場合には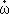=f（ω，i）という関係で表されるので、これを（11）式に示した動作点周りでTaylor展開し整理すると、次のような線形状態方程式を導くことができる。

　

　

ただし、

　

　

であり、

　

　

とする。ここで、導出された線形状態方程式（12）式は、係数が風速Vに依存しているために、風速Vに応じてシステムが変動することが分かる。

　

　モード2における制御目的は、カットイン風速Vciから定格風速Vratedの間の領域において、風エネルギーの獲得を最大にすることである。よって、Fig. 5に示すように、動作点としては風力発電機の出力係数CPが最大となる点を動作点（λ^*＝λopt）とする。この時、風速Vに対する最適回転数ω^*は、周速比の関係より以下のように表現される。

　

　

　

ゆえに、制御目的は次のように表される。

　

　

　モード2では、動作点における周速比は常に動作点（λ^*＝λopt）で一定であるので、（12）式は風速Vに線形に依存したモデルであることが分かる。さらに、風速Vの変動域がカットイン風速Vciから定格風速Vratedまでの間であることを考慮すると、線形補間タイプのモデルとして、次のようなLPVモデルが導出される。

　

　

　ただし、

　

　

　本論文ではLPVコントローラを設計する際、混合感度問題をべースとして制御系設計問題を考慮するために、Fig. 6に示す制御システム構造を用いる。ここで、WIとWDはそれぞれ積分重み、微分重み、ωcは回転数指令信号、zは制御評価信号、yは観測出力を意味する。上記の制御システム構造について、拡大系を構成すると次のようになる。

　

　

　

ただし、

　

　

　上記のモデルに対して、以下に示す制御仕様を満足する極配置制約付きLPV出力フィードバックコントローラを設計する。

　

　すべての制御仕様はLMI（線形行列不等式）として実現されるので、カットイン風速Vciの時と定格風速Vratedの時のそれぞれ端点での数学モデルに対してLMIを作成し、すべてを同時にγを最小化する準最適化問題として解くことにより、LPVコントローラを設計する^8）。