|
2.3 同化手法の検討
本項では、平成16年度事業「台風時の内湾海上風推算の研究」で課題として挙げられた同化手法について検討を行った。ここで、同化手法とは、解析値や観測値の情報を数値予報モデルに同化し、より精度の高い推算を行う処理である。
平成16年度事業「台風時の内湾海上風推算の研究」では、同化手法はMM5に付属のSatuffer and Seaman(1990)の開発した解析値ナッジング(nudging)を使用していた。この手法の概要と、この手法を用いた計算結果について示す。
(1)概要
この手法は、タイムスステップ毎に解析値や観測値の持つ有効な情報を外力として与える連続同化手法であり、オーストラリア気象研究センター(BMRC)の熱帯解析予報システム(TAPS)などで、現業運用されている。
ナッジングに使用する方程式を式(2.17)に示す。αi(x,t)は、予報変数を示し、風、気温、比湿などである。Fは予報式で、予報変数に変化を与えるすべての物理過程を含み、時間・場所などに依存して変化する。右辺第2項はナッジング項であり、予測値と解析値との差を外力として加える。Gはナッジング係数で、解析値へどの程度近づけるかを決める係数であり、解析値の精度と計算値の精度のバランス、解析値の時間密度に依存する。
この手法を使用することにより、今まで初期値・境界値のみに解析値の情報が反映されていたが、推算期間は外力として解析値の情報を反映させることができる。台風推算においては、解析値やベストトラックの情報を同化することにより、台風進路の誤差を小さくする効果を期待できる。
αi(x,t):予報変数
αia:予報変数の解析値
F:予報式
G:ナッジング係数(−)
(2)これまでの同化手法を用いた計算
これまでの同化手法(ナッジング)の、(1)T9918におけるナッジング係数の調査、(2)6事例におけるナッジングの精度検証について調査した。
・台風9918号におけるナッジング係数の調査
4次元同化(ナッジング)は、ナッジング係数を大きくすると、推算値を解析値に近づけるため、進路推定の精度などが向上する傾向がある。一方で、ナッジング係数を大きくすると、強制的に解析値になじませるため、推算値にスムージングをかける効果があり、台風の中心気圧が減衰し、台風の気圧深度の推算精度を悪化させる傾向がある。したがって、4次元同化(ナッジング)を行う場合は、進路推定誤差を小さくしようとすると気圧深度誤差が大きくなり、気圧深度誤差を小さくしようとすると進路推定誤差が大きくなるというトレードオフの関係になるため、ナッジング係数を適切に選択する必要がある。
そこで、T9918を対象に、ナッジング係数を変化させ、それぞれのナッジング係数によって台風の進路と気圧深度の推算精度がどのように変化するか調査を行った。
計算は、初期を台風が八代海・周防灘を通過する36時間前の1999年9月22日とし、推算時間は36時間とした。ナッジングは、解析値を3時間ごとに作成し、大領域、小領域の両方を対象に、風と気温を同化した。なお、大気境界層については、ナッジングを行わなかった。推算条件を表2.3に示す。
表2.3 推算条件
| 項目 |
内容 |
| 初期時刻 |
1999年9月22日21時 |
| 推算時間 |
36時間 |
| 要素 |
風、気温 |
| 高度 |
大気境界層以高 |
| 領域 |
大領域、小領域 |
| 係数(第1領域) |
2.5e-4、1.0e-4、2.0e-5、0.0e-6 |
| 係数(第2領域) |
2.0e-5、2.0e-6、0.0e-6 |
| 時間密度 |
3時間おき |
|
精度は、進路推定誤差と気圧深度推定誤差で評価した。進路推定誤差は、推算時間内における推算値とベストトラックの台風中心位置の平均2乗誤差(km)とし、気圧深度推定誤差は、推算時間内における推算値とベストトラックの気圧深度の平均2乗誤差(hPa)とした。ナッジング係数ごとの進路推定誤差と気圧深度推定誤差を図2.17に示す。
進路推定誤差は、ナッジングを行わない場合(第1・第2領域ともナッジング係数0)がもっとも大きく、110kmの誤差が生じていた。第1領域、第2領域ともに、ナッジング係数を大きくすると進路推定誤差は小さくなり、第1領域1.0e-4、第2領域2.0e-6で60km弱になった。しかし、それ以上係数を大きくしても、進路推定誤差はほとんど変化しなかった。
気圧深度推定誤差は、ナッジングを行わない場合(第1・第2領域ともナッジング係数0)がもっとも精度が良く、誤差は8hPaであった。第1領域、第2領域ともに、ナッジング係数を大きくすると台風は減衰し、気圧深度推定誤差は大きくなった。台風の減衰は、第2領域はナッジング係数を上げると大きくなったが、第1領域の係数を1.0e-4以上に大きくしても、変化しなかった。
図2.17 ナッジング係数と推算精度
(左:進路推定誤差、右:気圧深度推定誤差)
ナッジングは、ナッジング係数を適切に決めることが重要で、ナッジング係数は進路推定誤差と気圧深度推定誤差のかね合いで決定する必要がある。進路推定誤差を小さくするべき時はナッジング係数を大きくする方が良く、気圧深度誤差を小さくするべき時はナッジング係数を小さくする方がよい。ただし、ナッジングを行っても気圧深度を十分再現できる事例であれば、ナッジング係数は大きく設定してもよい。
本研究では、進路推定誤差が小さく、気圧深度推定誤差も大きくならない係数という観点から第1領域は1.0e-4、第2領域は2.0e-6とした。
・6事例におけるナッジングの精度検証
前項で設定したナッジング係数を用いて、データ同化(ナッジング)を用いた場合と用いない場合の精度比較を行った。対象台風は、2.1.3項と同様に、1996年から2004年に八代海・周防灘に高波をもたらした6事例(T9711、T9719、T9918、T0215、T0416、T0418)とした。推算計算は、2.1項に記述した領域、計算OPTIONで行い、推算時間は36時間とした。データ同化は第1領域、第2領域両方に行い、解析値はベストトラックデータの存在する3時間ごとに台風ボーガスを投入して作成した。
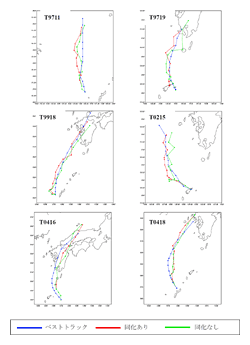
図2.18に、各台風の推算時間毎における、(1)ベストトラック、(2)データ同化あり、(3)データ同化なしの台風進路を示す。また、図2.19にそれぞれの手法について6事例を平均した推算時間ごとの進路推定誤差を示す。
データ同化を行った場合は、T9719、T9918、T0215で進路推定の精度が向上していた。特にT9719では、推算時間36時間で、データ同化を行わなかった場合は北東に約60Km外れていたが、データ同化を行った場合は、ほぼベストトラックを再現していた。一方、T9711、T0416、T0418はデータ同化を行った場合も行わなかった場合と大きな差異はなかった。
6事例の平均は、データ同化を行った場合は、データ同化を行わなかった場合と比較して進路推定誤差は小さくなった。誤差は、推算時間が進むにつれて、データ同化を行わなかった場合の方が大きくなり、推算時間36時間では、データ同化を行わなかった場合は約100kmの誤差で、行った場合は約80kmの誤差であった。
以上から、データ同化を行うことで進路推定誤差は小さくすることができると考えられる。
図2.18 推算時間ごとの台風進路推定誤差
図2.19 各事例のベストトラックと台風進路推算値
| (拡大画面:74KB) |
 |
|
|