|
1)モデルの方程式
ANKOUのように入射補角が20度〜90度と広い範囲の音響画像を扱うモデルとしては、堆積層からの体積散乱も考慮したComposite Roughness + Volume Scatteringモデルが有効である。
このモデルによると、音波の散乱強度Si(θ)は、
で表すことができる。
ここで、σγ(θ)は海底の凹凸による散乱であり、σν(θ)は海底の堆積層からの散乱である。両者は完全に独立しているわけではないが、底質及び凹凸をパラメータで表すと、二つに分類した方が考えやすい。
(1)堆積層からの散乱
堆積層内からの散乱は、一般に堆積物の密度と音速の比(音響インピーダンス)の変動によって与えられ、密度ρ及び音速Cで表すことができる。音波は海底での水と堆積物との境界面において、反射や屈折が起きる。これは堆積層の密度と音速に依存し、海水の密度と水中での音速比としてv、ρとする。
海底境界面からの散乱は、緩やかな入射補角(20度〜70度)では、海底面からの散乱ではなく、むしろ堆積物中に入射した音波が、体積層で散乱して戻ってくるものである。
これは次式で求められる。
ここで
である。 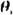 は平らな境界面に沿った音波の屈折角を表す。 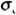 は体積中での散乱断面積、 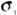 は堆積物中での減衰係数をしめす。
(2)海底面の凹凸による散乱
音波の散乱は海底面の凹凸にも依存する。海底面では、音波の周波数に比べて波長の短い凹凸と、波長の長い凹凸が存在する。このため両者は個々に扱われる。波長の短い凹凸(細かい凹凸)は、平均海底面の凹凸を基準とした実際の海底面の変位位置ベクトルとしてh(r)として表す。海底の凹凸が一様でその分布がgaussianであるとすると、
のように波数を用いて周波数特性が表現できる。ここでγ=3〜4であり、通常は3.5を用いる。海底面の凹凸h(r)は、構造関数パラメータα及びChを用いて次式で表せる。
ここで
Rayleigh-Rice近似
細かい凹凸における後方散乱強度はRayleigh-Riceによって求められる。海底から距離rの点における音波の後方散乱強度Sbは、入射音波の強度をIo、散乱強度をIs、照射面積をAとすると次式で定義される。
Kaを音波の波数として入射角θに対する散乱断面積 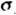 は次式で求められる。
ここでFは臨界角θc、を使って下記のように示すことができる。
Composite Roughness + Volume Scatteringモデル
スケールの大きい凹凸の場合には、Reyleigh-Rice近似では入射補角が異なる。これをスケールの傾きχの実効値(rms)をsとして入射補角が局所的に変化するものとして平均すると、
とあらわせる。
ここで関数Rはスケールの大きい凹凸のために生じる影を考慮したもので、
ここで
|