|
4.4.4 浸水量の推定
4.4.4.1 浸水量の推定式
先に述べた実験結果より,模型内水面の位置によって,浸水速度を推定する式を使い分ける必要がある。図4.4-12に区分すべき模型内水面位置を示す。
図4.4-12 Location of opening and flood water depth.
詳しくはAppendixで説明するが,Bernoulliの定理より,各状況での流入量を推定するために用いる式は以下のようになる。式中で用いた文字は図4.4-12の中で示している。なお,簡単のため空気圧縮は考えていない。ここで,Cは流量係数と呼ばれる破口における摩擦抵抗や流水断面積が拡大するときにその外側に渦が発生することによる損失を考慮するための係数である。
(a)破口の高さ中心に喫水線上にある場合
(b)破口が完全に水面下にある場合
4.4.4.2 流量係数の推定
実験結果より,各流量係数を求めた。結果を表4.4-1に示す。なお,流入量が境界において急激に変化する様子が見られなかったので,C1=C21,C22=C3とした。
小型模型と大型模型で流量係数に違いが見られる。このことから,流量係数には尺度影響が存在することがわかる。模型船を用いて浸水実験を行う場合には,流量係数がほぼ等しくなるような縮尺で,実験を行う必要があると考えられる。
一方,サイズが等しく,コンディションが異なる場合を比較すると,流量係数はほぼ等しい。
表4.4-1 Coefficients of discharge
| size |
condition |
C1=C21 |
C22=C3 |
| small |
a |
0.663 |
0.60 |
| small |
b-1 |
0.654 |
0.60 |
| large |
a |
0.555 |
0.53 |
| large |
b-1 |
0.560 |
0.53 |
|
表4.4-1の流量係数と(1)〜(5)式(多方程式モデル)を用いて,シミュレーションを行なった。
図4.4-13〜16に,本実験結果,前述の推定式による計算結果および現在広く用いられている簡易推定式(1方程式モデル)による計算結果を比較して示す。
なお,それぞれの図中の右図は,最終状態付近の拡大したものである。
図4.4-13 Time history of simulated and measured flood water depth in small model under condition (a).
|
(拡大画面:11KB)
|
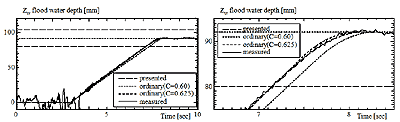 |
図4.4-14 Time history of simulated and measured flood water depth in small model under condition (b-1).
|
(拡大画面:11KB)
|
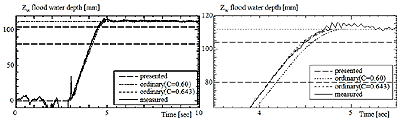 |
図4.4-15 Time history of simulated and measured flood water depth in large model under condition (a).
|
(拡大画面:11KB)
|
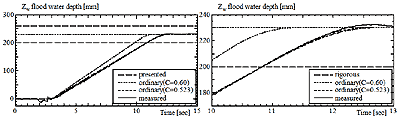 |
図4.4-16 Time history of simulated and measured flood water depth in large model under condition (b-1).
|
(拡大画面:10KB)
|
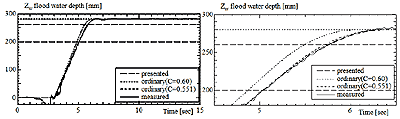 |
多方程式モデルの計算結果と実験結果を比較すると,非常に良く一致している。しかし,慣性力について考慮していないため,流入の最終状況において,流入量にわずかの違いが見られ,オーバーフローなどは再現できていない。
また,1方程式モデルを用いる際,流入係数C=0.60とするのが一般的であるが,C=0.60としたときの計算結果は実験結果と大きく異なっている。しかし,模型内水面が破口下端に達するまでの流量一定である範囲から,流量係数Cを求め,その値を用いると,簡易推定式でも良い一致を示している。
それぞれの推定法を用いた結果と比較すると,喫水付近において,1方程式モデルの方がわずかだが流量が多い。これは,破口下端よりも模型内水面が高くなった場合に流量係数が小さくなることを考慮していないためだと考えられる。
4.4.5 結言
以上の結果から,以下の結論が得られた。
1. 流量係数Cには尺度影響がある。
2. 浸水する区画から流出する空気の速度によって,流量に違いがある。
3. 模型内水面が流入口の下端に達すると,流量係数が小さくなる。
4. 1方程式モデルと多方程式モデルの結果にはわずかな差異が見られる。その差は模型スケールが小さくなるほど顕著に現れる。1方程式モデルでは流入速度を過大評価する傾向にある。
5. 今回実施した実験においては,空気圧縮によって流入速度が遅くなることもまた確認できたが,空気圧縮に関する詳細な検討は行うことができなかった。今後の検討課題であると考えている。
参考文献
1)Yoshiho Ikeda, Shigesuke Ishida, Toru Katayama, and Yuji Takeuchi: Experimental and Numerical Studies on Roll Motion of a Damaged Large Passenger Ship in Intermediate Stages of Flooding, Proc. of 7th International Ship Stability Workshop, pp.42, Shanghai, 2004.
2)片山徹,武内祐二,池田良穂:巨大客船の損傷時浸水中間段階における挙動に関する実験的研究,関西造船協会講演概要集,秋季造船三学会連合大会,2004.11.
3)池田良穂,瀬崎良明,高橋俊次郎:損傷時復原性基準とその理論的背景,試験水槽シンポジウム 操縦性および復原性基準に関する研究の動向(日本造船学会),平成12年12月。
4)R.v.Veer, W.Peters, A.Rimpela and J.d.Kat: Exploring the influence of Different Arrangements of Semi-Watertight Spaces on Survivability of a Damaged Large Passenger Ships, Proc. of 7th International Ship Stability Workshop, pp.30, Shanghai, 2004.
5)L. Palazzi, J.d.Kat: Model Experiments and Simulations of a Damaged Ship With Air Flow Taken Into Account, Marine Technology, Vol.41, No.1, 2004.1.
|