|
図2.8
|
風向風速分布図
黒丸:台風中心 黒矢印:台風進行方向 上:2次元台風モデル、下:観測(2次元台風モデル:9月22日18時JST、観測:9月22日18時15〜18分JST)
|
(4)八代海・周防灘における計算値と観測値の比較
八代海・周防灘において、これまでの推算手法による計算値と観測値の比較を行った。
計算は、初期値を1999年9月22日21時として、48時間の推算を行った。計算に用いた台風パラメータを表2.3に示す。緯度・経度、中心気圧は、気象庁発表のベストトラックデータを使用した。最大風速半径は、Myersの式(2.1)を用い、1000hPaの等圧線までの平均距離から求めた。ただし、台風中心が九州地方に接近した9月24日3〜12時は、九州地方の気象官署の気圧観測値を用いて求めた。周辺気圧との差は周辺気圧を1010hPaとして算出した。
表2.3 計算に用いた台風パラメータ
| 月日 |
時間
(JST) |
経度
(deg) |
緯度
(deg) |
中心気圧
(hPa) |
最大風速半径
(km) |
周辺気圧との差(hPa) |
| 9月22日 |
21:00 |
127.2 |
26.3 |
930 |
34 |
80 |
| 9月23日 |
3:00 |
127.2 |
27.0 |
930 |
39 |
80 |
|
9:00 |
127.3 |
27.8 |
930 |
34 |
80 |
|
15:00 |
127.8 |
28.9 |
935 |
38 |
75 |
|
21:00 |
128.6 |
30.4 |
935 |
41 |
75 |
| 9月24日 |
3:00 |
129.7 |
31.7 |
935 |
60 |
75 |
|
6:00 |
130.5 |
33.0 |
950 |
61 |
70 |
|
8:00 |
131.2 |
33.8 |
950 |
69 |
60 |
|
9:00 |
131.3 |
34.3 |
960 |
73 |
50 |
|
12:00 |
132.6 |
35.7 |
965 |
80 |
45 |
|
15:00 |
133.7 |
37.1 |
965 |
64 |
45 |
|
21:00 |
137.0 |
40.0 |
970 |
96 |
40 |
|
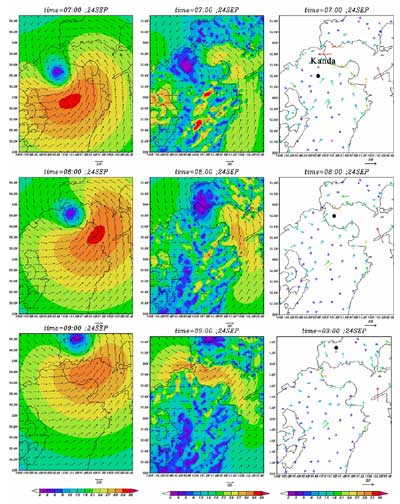
T9918が周防灘付近を通過した9月24日7〜9時の計算結果と観測結果の風速分布図を図2.9に示す。計算結果は、2次元台風モデルと、Masconモデルによる高度10mにおける風速分布と風ベクトル図を示す。観測値は、AMeDAS観測地点と、表1.1の観測地点における、風ベクトル図を示す。(風速で色分け)
2次元台風モデルの計算値は、台風の中心付近では、最大風速地点と台風中心を結ぶ線に対して線対称の風速分布であった。Masconモデルの計算値では、地形の影響を評価し、地形に沿った風速分布を推算した。とくに、(1)周防灘など地形の収束する地域や、(2)九州山地など標高の高い地点に向かって風が吹き込む地域では、風速が大きくなった。
台風が通過した周防灘北部の苅田港に着目して、観測値と計算値の風速の時系列変化を比較した。対象地点の観測値、2次元台風モデル計算値、Masconモデル計算値の時系列図を図2.10に示す。苅田港の観測値は、第4港湾建設局の観測値(苅田2)に欠測があったため、福岡県の観測値(苅田1)を使用した。計算値は観測高度の30mに換算して描画した。
観測値では、台風通過前の24日7時に風速39.5m/s、通過時の8時に20.7m/s、通過後の9時に26.1m/sと、台風通過前に最も強かった。これは、台風の後面より前面に強風域が存在していたことを意味している。しかし、2次元台風モデル・Masconモデルの計算値は、通過前より通過後に最も強い風速を計算した。図2.9の24日7時の風速分布図でも、Masconモデルは台風の前面の周防灘南部に強風域を計算しているが、苅田港では強風域を計算しなかった。
T9918は洋上と同様に、八代海・周防灘を通過する時にも台風の前面に強風域があった。しかし、これまでの推算手法は、地形の影響を評価することのできるMasconモデルでも、前面の強風を再現することができなかった。したがって、T9918事例の海上風を推算するためには、台風の非対称性を評価することのできる計算を行う必要があると考える。
|
図2.9
|
T9918の計算値の風速分布・風ベクトル図と観測値の風ベクトル分布図
左:2次元台風モデル、中:Masconモデル、右:観測値(黒丸は台風中心位置)
|
|
(拡大画面:229KB)
|
 |
|
図2.10
|
苅田港における観測値、2次元台風モデル、Masconモデルの時系列風速分布
(OBS: 観測値、2D: 2次元台風モデル、MAS: Masconモデル)
|
本章では、数値予報モデルを使った推算手法について検討を行った。数値予報モデルは、ペンシルバニア州立大学と米国大気科学センターにより開発されたメソ気象モデルMM5を使用した。
検討は、2004年の台風事例を対象に、計算OPOTION、初期値・境界値の検討を行い、T9918事例を対象に台風ボーガスやデータ同化(ナッジング)、解像度の検討を行った。検討フロー図を図3.1に示す。
図3.1 数値予報モデルを使った推算手法の検討フロー図
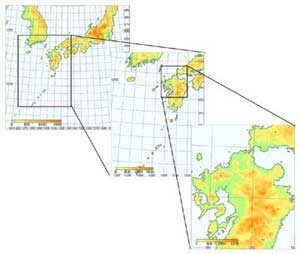
推算計算には、図3.2に示す計算領域を用いた。計算領域1(大領域)は、水平解像度13.5km×13.5kmで140×140の格子数からなり、台風を含む環境場を覆い、台風の移動を推算する。大領域の計算結果により、計算OPTIONの検討、初期・境界値の検討を行った。中領域は、4.5km×4.5kmで241×181の格子数からなり、台風全体を含む領域を覆い、台風の内部構造を解像できる。大領域と中領域の2way-nestingにより、台風ボーガスの検討やデータ同化(ナッジング)の検討を行った。小領域は、1.5km×1.5kmで181×151の格子数からなり、八代海・周防灘を覆い、複雑な地形を詳細に表現することができる。大領域、中領域、小領域の2way-nestingにより、解像度の検討を行った。各領域とも、鉛直方向には、最下層をσ=0.997、最上層を70hPaとして、計36層を置いた。
図3.2 計算領域
(左:大領域、中:中領域、右:小領域)
|
(拡大画面:76KB)
|
 |
メソ気象モデルMM5は、目的によって計算スキームを選択することができる(計算OPTION)。各計算スキームごとに計算時間は変化し、高度なモデルを用いると計算時間が増大する傾向がある。一方、台風時の内湾海上風推算の調査にはできる限り計算負荷の軽いモデルが求められている。計算OPTIONによる、精度、計算負荷について2004年の台風事例を対象に調査を行った。
気象モデルMM5は、微物理、積雲パラメタリゼーション、大気境界層、放射、地表面過程など様々な物理過程を考慮している。このうち、微物理、積雲パラメタリゼーション、大気境界層は台風の進路推算に大きな影響を持っている。本章では、この3つの物理過程について検討を行った。
メソ気象モデルMM5において、微物理、積雲パラメタリゼーション、大気境界層で選択可能なOPTIONを表3.1に示す。表3.1のOPTIONから、計算負荷が小さく、かつ精度の高いOPTIONの選択を行った。
表3.1 気象モデルMM5の各物理過程OPTION
|
微物理 |
積雲パラメタリゼーション |
大気境界層 |
| 1 |
Dry |
None |
No PBL |
| 2 |
Stable |
Kuo |
Bulk |
| 3 |
Warm rain |
Grell |
Blackadar |
| 4 |
Simple ice |
Arakawa-Schubert |
Burk-Thompson |
| 5 |
Mix phase |
Fritsch-Chappell |
Eta PBL |
| 6 |
Graupel(gsfc) |
Betts-Miller |
MRF |
| 7 |
Graupel(reisner2) |
Kain-Fritsch |
Gayno-Seaman |
| 8 |
schultz |
Kain-Fritsch2 |
Pleim-Xiu |
|
検証計算は、2004年の台風事例で台風中心が日本付近に接近したT0415、T0416、T0418、T0421、T0422、T0423を対象とした。台風が日本付近に最接近したあるいは上陸した36時間前を初期値として、48時間の推算を行った。各台風事例の初期時刻を表3.2に示す。
表3.2 検証台風事例の初期時刻
|
台風名 |
初期時刻 |
| 1 |
T0415 |
8月17日21時 |
| 2 |
T0416 |
8月28日21時 |
| 3 |
T0418 |
9月5日21時 |
| 4 |
T0421 |
9月27日21時 |
| 5 |
T0422 |
10月7日21時 |
| 6 |
T0423 |
10月18日21時 |
|
微物理、積雲パラメタリゼーション、大気境界層のOPTIONごとの計算精度と計算負荷を調査した。計算精度は、推算計算結果の台風中心位置のベストトラックからの誤差(進路推定誤差 式3.1)とベストトラックとの気圧深度の誤差(気圧深度誤差 式3.2)で評価した。進路推定誤差、気圧深度誤差は、推定要素として以下の理由から重要である。
・台風は中心部に強風域が集中しており、台風中心部との距離に風速は依存する
・台風は中心に対する相対的位置に風向や風速が依存する
・台風の最大風速は、気圧深度に依存する
計算結果の台風中心位置は、海面気圧がもっとも低い位置として算出した。
NT :ベストトラック該当時刻数
xb,yb :ベストトラック台風位置
x,y :推算値台風位置
Pb :ベストトラック気圧深度
P :推算台風気圧深度
(1)微物理
微物理過程は、MM5には8種類のOPTIONが用意されている。DryやStableは、降水を予報しないため、台風の構造を表現することができない。Warm Rainは、氷相を考慮しないが、台風の雲は高度10kmにも達し氷相の雲粒で形成されているため台風の推算には適切でない。したがって、Dry、Stable、Warm Rain以外の5種の計算OPTIONについて検討を行った。
表3.3に、各OPTIONごとの計算負荷と進路推定誤差と気圧深度誤差を示す。計算負荷はsimple iceを1とした推算時間とした。進路推定精度はsimple iceで93.3km、気圧深度誤差は10.4hPaであった。高度なOPTIONを使うことで計算負荷は増加するが、進路推定精度・気圧深度誤差はあまり変わらなかった。したがって、大領域ではsimple iceを使用した。しかし、格子間隔5km以下では、鉛直速度が粒子の落下速度と同程度になるため、微物理過程は重要になることが報告されている。(Christopher A.Davis 2001)したがって、中領域・小領域ではあられを考慮したOPTIONであり、計算負荷の軽いGraupel(reisner2)を使用した。
表3.3 微物理のOPTION毎の調査結果
| 項目 |
内容 |
推算 |
計算負荷 |
気圧深度誤差
(hPa) |
進路推定誤差
(km) |
| 大 |
中 |
| Dry |
ドライモデル |
× |
× |
- |
- |
- |
| Stable |
非対流性降水のみ |
× |
× |
- |
- |
- |
| Warm rain |
氷相を考慮しないモデル
混合比qc,qrを予報 |
× |
× |
- |
- |
- |
| Simple ice |
氷相を考慮するモデル
混合比qc,qr,qi,qsを予報
過冷却なし |
○ |
× |
1 |
10.4 |
93.3 |
| Mix phase |
氷相を考慮するモデル
混合比qc,qr,qi,qsを予報
過冷却あり |
○ |
× |
1.65 |
10.7 |
91.1 |
Graupel
(gsfc) |
氷相を考慮するモデル
混合比qc,qr,qi,qs,qgを予報 |
○ |
○ |
1.71 |
7.2 |
103.2 |
Graupel
(reisner2) |
氷相を考慮するモデル
混合比qc,qr,qi,qs,qg、
数濃度をNi,Ngを予報 |
○ |
○ |
1.28 |
9.9 |
88.6 |
| schultz |
氷相を考慮するモデル
混合比qc,qr,qi,qs,qgを予報 |
○ |
○ |
1.53 |
7.9 |
90.6 |
|
|