|
河川断面の測り方
流速がわかっても河床の断面がわからなければ、流量の計算は出来ません。川底が平面であれば川幅と水深を測って川幅×水深×流速=流量(m3)となりますが、およそ川底の一定の所というと橋の下や落差工を除いてはありません。川は底が狭く、上部は広い踏み台を逆さにした形をしています。そこで普通は台形の計算式を使い、(川底+川面)×水深÷2で計算します。しかし自然の流れは複雑ですから川底の状況に応じて断面積を計算しなければなりません。
一般的な流量の計算法:流量Q、流速V、断面積nmとすると、
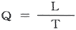 nm、単位cm/secで求められます。 (流速Vは、時間T分の距離Lで測ります。)
断面積(A)の求め方:
ここに2001年7月8日(日)、東村山第三中学校自然科学部(木村甫先生指導)の生徒たちと行った流量測定結果を、当会 宮下博文氏の報告と第三中学校生徒の報告を併せて報告いたします。
第一回 流量測定報告 宮下博文
7月8日、梅雨の中休みに第一回空堀川流量測定を行いました。
当地は2日前、小雨がパラついていたが、前日からは快晴に恵まれ、測定作業には好条件でした。前日、小林会長と一緒に調査地点の下見を行い、浄水橋上流から下流の空堀川と西武池袋線交差部まで歩き、候補地点四か所を絞りました。当日は第一、第二候補地の状況が比較的良好なためと、第三、第四候補地は水量不足で測定不可能と認め2か所に決めました。
流量測定に参加したのは、講師として招いた東京都環境科学研究所の大野氏と東村山第三中学校の木村先生と生徒12名、当会から小林、斎藤、宮下の3名でした。
西武新宿線久米川駅に9時集合し、川沿いを歩いて空堀広場から東村山浄水場脇に行き、ここで測定の説明をして第一現場に下りました。
・作業手順として
(1)測定準備 (2)川の断面積の測定 (3)流速の測定
以上の手順で行い、測定値等交え次に説明させていただきます。
◎第一現場:浄水場上流50m地点の水深15cm程度、水面が緩やかに流れる場所を選びました。(川まつりの時ボートを浮かべた場所)
(1)測定準備 長さ15mの伸びの無い紐に1mごとにマジックインキで印しをつけ、5mごとに黄色い紐をつけ紐尺を作り、準備作業を終了。
(2)川の断面積の測定
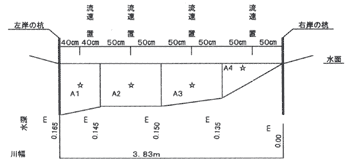
| (ア) |
川の流れに直角に、両岸の水際に1本づつ木杭を打ち込み、杭間に紐尺を水平にはる。 |
| (イ) |
右岸より1mごとに水深を測り(0.00m、0.135m、0.150m、0.145m、0.165m)記録する。 |
上記作業で下記の流水断面を得る。
| (拡大画面:10KB) |
 |
| (ウ) |
右岸A4、A3、A2、A1それぞれブロックの中心で水深60%の深さで流速係数(☆印)r.p.mを測定し、記録する。 |
測定結果 (表の中の数字は流速係数r.p.m)
| |
A1 |
A2 |
A3 |
A4 |
| 第1回 |
434 |
191 |
145 |
283 |
| 第2回 |
441 |
418 |
219 |
224 |
| 第3回 |
626 |
266 |
334 |
285 |
| 第4回 |
693 |
469 |
0 |
229 |
| 第5回 |
424 |
232 |
0 |
373 |
| 計 |
2618 |
1576 |
698 |
1394 |
| 平均流量係数(x) |
523.6 |
315.2 |
232.6 |
278.8 |
| 平均流速 |
0.1266 |
0.0964 |
0.0844 |
0.0911 |
| 断面積 |
0.124 |
0.148 |
0.143 |
0.068 |
| 平均流量 |
0.0157 |
0.01427 |
0.01207 |
0.0062 |
|
(3)平均流速の計算 y=0.0145x+5.07(平均流速の単位cm/sec)
流量計算
A1 断面積(0.124)×平均流速(0.1266)=0.0157(m3)
A2 断面積(0.148)×平均流速(0.0964)=0.0142(m3)
A3 断面積(0.143)×平均流速(0.0844)=0.0120(m3)
A4 断面積(0.068)×平均流速(0.0911)=0.0062(m3)
流量の合計 A1+A2+A3+A4=0.048m3 0.048×1000=48リットル
◎第二現場:第二砂川橋下。東村山浄水場下流250mの第二砂川橋下の水深30cm程度、水面がスムーズに流れている場所で行った。(下見の場所)
(1)測定準備 第一現場と同じ。
(2)川の断面積の測定
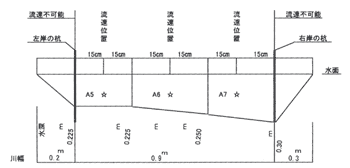
| (ア) |
第一現場同様に両岸に各々1本づつ木杭を打ち込み、杭間に紐尺を張ったが流速不能箇所があったので、川幅140cmの内側右岸より30cm範囲と左岸20cm範囲を切り捨て、測定範囲を90cmとした。両端はほぼ水の動きは無かった。
右岸から30cmの地点と120cmに杭を打ち流速測定範囲にて再測定し下記の結果を得た。上記作業で得た流水断面は下図の通りである。 |
| (拡大画面:11KB) |
 |
| (イ) |
左岸 A5からA7のブロックの中心で60%の深さで流速係数(☆印)r.p.mを測定し、記録する。 |
測定結果 (表の中の数字は流速係数r.p.m)
| |
A5 |
A6 |
A7 |
| 第1回 |
962 |
824 |
561 |
| 第2回 |
1315 |
1022 |
0 |
| 第3回 |
0 |
1980 |
0 |
| 第4回 |
0 |
1899 |
0 |
| 第5回 |
0 |
0 |
0 |
| 計 |
2277 |
5725 |
561 |
| 平均流量係数(x) |
1138.5 |
1431.25 |
561 |
| 平均流速 |
0.2157 |
0.2582 |
0.1320 |
| 断面積 |
0.068 |
0.071 |
0.083 |
| 平均流量 |
0.0146 |
0.0183 |
0.01095 |
|
(3)平均流速の計算 y=0.0145x+5.07(平均流速の単位cm/sec)
流量計算
A5 断面積(0.068)×平均流速(0.2157)=0.01467
A6 断面積(0.071)×平均流速(0.2582)=0.0183
A7 断面積(0.083)×平均流速(0.132)=0.0109
流量の合計 A5+A6+A7=0.043m3 0.043×1000=43リットル
結論として、上流の48リットルに対して、下流の43リットルの結果は、下流の測定不可能箇所でいくらかの流れ(5リットル/sec)があったものと考えられる。
上記5リットルが浸透水であれば250mの間で浸透していると考えたが、浸透する区間はないように見える。
第一現場の測定はほぼ正しいと思われるので、今後定期的に測定することで浸透の有無はわかるであろう。
第三、第四現場での測定は水量不足で断念した。
|