|
7. 交流
7・1 単相交流の発生
交流とはどのような形の電気かについては1・12・2で簡単に述べたが、さらに詳しく考えてみよう。
図7・1
図7・1は簡単な交流発電機の原理図である。
図7・1(a)において、N極からS極に向っている強力な磁界中にABCDなるコイルをある回転速度で回転すれば、2・4で説明したとおり誘導起電力がコイル中に発生し、負荷Lに電流が流れる。そこで、この電流の流れ方をみる。
図7・1(a)においては、ABCD−R2−B2−L−B1−R1−ABの順序となる。このコイルが180°回転すれば、電流の流れが逆になって図7・1(b)のようにDCBA−R1−B1−L−B2−R2DCのような順序となる。この流れの形をさらに図7−2についてみよう。
ここで、R1及びR2の環をスリップリング(集電環)といい、B1及びB2をブラシ(刷子)という。
| (拡大画面:21KB) |
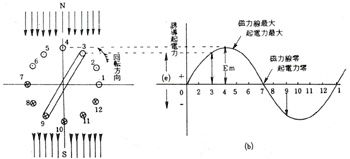 |
図7・2
図7・2(a)はDCBAコイル(図7・1(b)参照のこと。)が磁界中の磁力線を切っている状態であって、そのために誘導される起電力の変化の状態が図7・2(b)に曲線として示されたものである。
次にsinθ又は(6・3)式によりsinωtの曲線を図示してみよう。図7・3(a)においてOA=1としてsinθ=ABにおけるABの値を数表により求める。(sinθのθの値に図7・3(a)のように代入する。)このように求めた値が図7・3(b)の曲線になる。
| (拡大画面:22KB) |
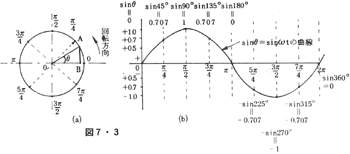 |
図7・3
この曲線を正弦波曲線(サインカーブ sine curve)という。
以上は解析的に説明したが、次のように作図的に考えてもよい。図7・3(a)において、Oを中心として腕OAが反時計式に回転しOAの正射影ABの長さが変わるが、その変り方を回転角に対応して描けば図7・3(b)のような曲線となる。よってこの曲線を正弦波曲線(サインカーブ)という。
そこで、図7・2の交流発電機の誘導起電力の波形と図7・3における正弦波曲線とは相似である。それ故に、この誘導起電力は正弦波曲線の式sin ωtを用いる。
図7・2(b)において、誘導起電力の最大値をEmとし、瞬時電圧をeで表せば、次の式が交流電圧の式である。
e=Em sin ωt〔V〕・・・(7・1)
ここで、ωは(6・4)式によって、
ω=2π/T〔rad/s〕である。
また、瞬時電流をiで表せば、次の式が交流電流の式である。
i=e/R〔A〕は交流回路の場合でもオームの法則が成り立つ。ただしRは抵抗とする。
|