|
4. 等価発電機の特性
母線における等価発電機は電動機寄与電流も合算して、その特性が検討される。
その交流分をIac(t)T0、直流分をIdc(t)T0とすると、夫々は次式で示される。
Iac(t)T0=ΣIGac(t)+ΣIMac(t)
Idc(t)T0=ΣIGdc(t)+ΣIMdc(t)
即ち、等価発電機の電流は電動機の寄与電流を含めた母線短絡電流と同一であることを示している。
尚、等価発電機関連の諸定数の記号文字は右片下に0点を付して示すこととする。
等価発電機の短絡電流の初期過渡電流成分をI″0、過渡電流成分をI′0で示すと、
等価発電機の交流分は
| (拡大画面:14KB) |
 |
任意の時間txにおけるしIac(t)0の値をK″(tx)0とすると
| (拡大画面:23KB) |
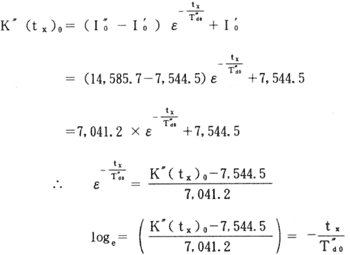 |
ここでt=(1/2サイクル時)=1/120〔sec〕とし、その場合の発電機と電動機の交流成分
電流値が算出済であるので、それ等の合算を行うと、
等価発電機の交流分の減衰定数T″d0は、
次に、等価発電機の直流分減衰時定数の値を求める。
直流分は発電機に対して、無負荷短絡時の1.03倍とみなすと、直流分の初期値I″dc0は次式で示される。
t=txの時点における直流分は
| (拡大画面:6KB) |
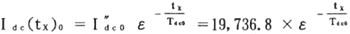 |
tx=1/2サイクル時におけるIdc(tx)0は
| (拡大画面:6KB) |
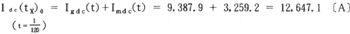 |
故に
等価発電機の直流分の減衰時定数Tdc0は
次に主母線から見た等価発電機のインピーダンスを求める。
初期過渡リアクタンスX″0は
過渡リアクタンスX′0は
抵抗分R0は
因みに等価発電機の1/2サイクル時のピーク値は前記の計算値より
等価発電機は発生電流の大きさが母線短絡電流と同じで、発電磯と電動機の双方の短絡電流特性を合成した1台の想定機械であることが理解される。
念のため、今回の計算例の場合、1/2サイクル時の値で示すと、下記の通りである。
| |
交流分実効値 |
ピーク値 |
| 発電機3台 |
7,929.9〔A〕 |
20,602.5〔A〕 |
| 電動機群 |
2,947.0〔A〕 |
7,426.9〔A〕 |
| 等価発電機 |
10,876.9〔A〕 |
28,029.4〔A〕 |
|