|
1・4 交流の測定量・電力
(1)実効値・最大値・平均値との関係
| (拡大画面:20KB) |
 |
| (2)波形率=実効値/平均値 正弦波では波形率= |
 |
≒1.11 |
全波整流型計器の指示(また目盛)
I=1.11Iav(正弦波の場合 Iav:平均値)
I=kIav(波形率kとなる交流の場合)
(3) 波高率=最大値/実効値 正弦波では 波高率= 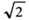 ≒1.414 〔例題〕交流電圧計の目盛で100〔V〕を指示した。最大値と平均値を求めよ。
〔解〕最大値= 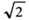 ×100=141.4〔V〕 平均値=0.9×100=90〔V〕
| (拡大画面:22KB) |
 |
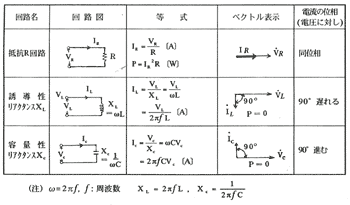
V:線間電圧(実効値)〔V〕、I:線電流(実効値)〔A〕
θ:電圧と電流との間の位相角〔rad〕、R:回路の等価抵抗〔R〕
Z:回路の等価インピーダンス〔Ω〕
(注)三相回路は正弦波平衡三相回路とする。
(1)等価抵抗 R=電力/(電流)2=Zcosθ
(2)等価インピーダンス Z= 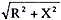 =電圧/電流=皮相電力/(電流) 2(3)等価リアクタンス X=Zsinθ=無効電力/(電流)2
電力量 P・t〔Ws〕又は〔J〕=電力×時間
P:有効電力〔W〕
以上は小さい値であるから、ワット×1,000=kW、秒×3,600=1hの単位が用いられる。それ故に電力量の単位は〔Wh〕又は〔kWh〕が一般に使用される。
〔例題〕1.60〔W〕の電球は10〔個〕つけた時流れる電流は何〔A〕か。また、これを10〔時間〕点灯すれば、電力量は何〔kWh〕か。ただし電圧は単相交流100〔V〕とする。
| 〔解〕I=P/V= |
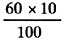 |
=6〔A〕 |
また、電力量=P・t=60×10×10=6,000〔Wh〕
=6〔kWh〕
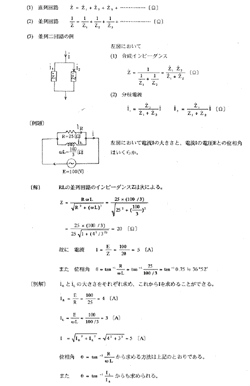
〔例題〕2. ある三相交流発電機の線間電圧、線電流を測定したら、それぞれ440〔V〕、500〔A〕であった。そして力率は80〔%〕であったという。その時の発電機の出力は何〔kW〕か。また皮相電力は何〔kVA〕か。
| (拡大画面:12KB) |
 |
〔例題〕3. 負荷に100〔W〕電球が70〔個〕、1(kW)の電熱器5〔個〕及び入力5〔kW〕の電動機3〔台〕がある。この場合の三相交流発電機は何〔kW〕の容量を必要とするか。
〔解〕出力 P=P1+P2+P3
=100×70+1,000×5+5,000×3
=7,000+5,000+15.000
=27,000〔W〕=27.0〔kW〕
| (拡大画面:8KB) |
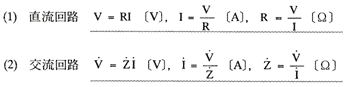 |
(注):(1)この法則は非線形回路では成り立たない。
(2) 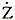 はインピーダンスでベクトル量である。
| (拡大画面:18KB) |
 |
〔例題〕インピーダンス 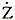 =4+j3〔Ω〕に電圧 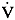 =100〔V〕を加えた時に流れる電流Iの大きさI〔A〕、位相角〔θ〕を求めよ。
| (拡大画面:9KB) |
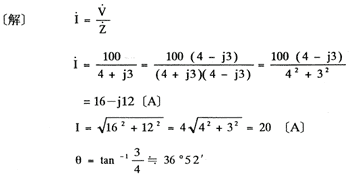 |
| (拡大画面:28KB) |
 |
| (拡大画面:23KB) |
 |
|