|
1・3 電磁誘導
| (1)基本式 e= |
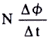 |
〔V〕 |
e:誘導起電力〔V〕、N:巻数、φ:磁束〔Wb〕、t:時間秒〔s〕、Nφ:鎖交数という
(注)△は微小値を表す符号
(2)平等磁界中を等速運動する導体の誘導起電力(フレミング右手の法則適用)
e=Blν〔V〕
B:磁束密度〔Wb/m2〕、l:導体の長さ〔m〕、ν:導体の速度〔m/s〕
e=Blνsinθ〔V〕
B:磁束密度〔Wb/m2〕、l:導体の長さ〔m〕
ν:導体の周辺速度〔m/s〕
θ:導体の運動方向と磁界の向きのなす角での角変位〔rad〕
e=Emsinθ=Emsinωt〔V〕
e:交流起電力の瞬時値、Em:交流起電力の最大値、θ:ωt〔rad〕
t:時間秒〔s〕、ω:角速度〔rad/s〕
1周波:1サイクル(正の半波と負の半波からなる1波形)
1周期T:時間秒〔s〕(1周波を完了するのに必要な時間)
周波数f:ヘルツ〔Hz〕(1秒間に繰り返される周波の数をいい周波数の単位にヘルツ〔Hz〕が用いられる。)
| (拡大画面:9KB) |
 |
(1)誘導起電力
| (拡大画面:3KB) |
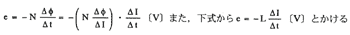 |
(2)インダクタンス(上式から)
| L=N |
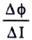 |
〔H〕 電流変化に応じて鎖交数(Nφ)の変化率 |
N:巻数、φ:磁束〔Wb〕、I:電流〔A〕、t:時間秒〔s〕、Nφ:磁束鎖交数
(1)相互インダクタンス
N1、N2:回路1、2の巻数
I1、I2:回路1、2の電流〔A〕、φ12、φ21:回路1→2、2→1への磁束数〔Wb〕
(2)自己インダクタンス
φ1、φ2:回路1、2のみの鎖交磁束数〔Wb〕
(3)MとLとの関係
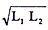 |
≧M12=M21〔H〕 |
(a)二つのコイル間に漏れ磁束がない場合
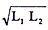 |
=M〔H〕 ここで M12=M21=M |
(b)二つのコイル間に漏れ磁束がある場合
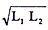 |
>M〔H〕 |
(c)一般
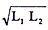 |
・k=M〔H〕 |
k:電磁結合係数
(4)相互誘導によって生じる起電力
〔例題〕1. 2二つのコイルがある。コイル1の電流が1/100〔s〕間に5〔A〕変化して、コイル2に23〔V〕の電圧を誘導するという。このときの両コイル1、2間の相互インダクタンスは何〔H〕か。
F=BIlsinθ〔N〕
F:力〔N〕、B:外部磁束密度〔Wb/m2〕
I:導体の電流〔A〕、l:導体の長さ〔m〕
θ:外部磁界の方向と導体の電流方向との角度〔rad〕
(1)直流の場合(空気中において)
F=2×10−7×l〔N〕
I1、I2:2導体の電流〔A〕、r:導体間隔〔m〕
l:導体の長さ(m〕
(注)I1、I2が同方向で吸引力、逆方向で反発力となる。
(2)交流の場合
| F=10−7× |
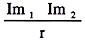 |
×l〔N〕 |
i1=Im1sin(ωt+θ1)〔A〕
i2=Im2sin(ωt+θ2)〔A〕
r:導体間隔〔m〕、(導体の直径に比べて極めて大きいものとする)、l:導体の長さ〔m〕
〔例題〕直流配電盤の母線に短絡電流が104〔A〕流れたとする。この場合における母線間の電流力は何ニュートン〔N〕か。ただし+、−母線間の距離は0.25〔m〕とし、長さは5〔m〕とする。
| (拡大画面:8KB) |
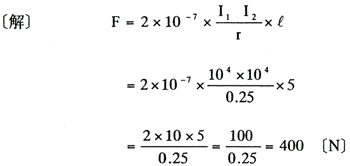 |
(注)1〔N〕=0.102〔kgf〕から
上記値=40.8〔kgf〕
(1)直流電磁石
| (拡大画面:4KB) |
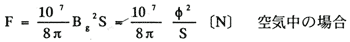 |
F:吸引力〔N〕、Bg:磁極相対端面における(空隙)磁束密度〔Wb/m2〕
φ:磁極相対端面の磁束〔Wb〕、S:磁極相対端面の断面積〔m2〕
(2)交流電磁石(平等磁界)
| (拡大画面:4KB) |
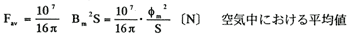 |
Fav:平均吸引力〔N〕、Bm:空隙の磁束密度最大値〔Wb/m2〕
S:磁極端面の断面積〔m2〕、φm:空隙の磁束最大値〔Wb〕
(注)交流電磁石の吸引力は交流励磁の周波数の2倍周波数で脈動する。
|