|
7・5 単相交流の電力と力率
図7・47
図7・47の抵抗回路の電力について計算しよう。電力は5・3で述べたとおりP=V・1〔W〕であるから、交流の場合の電力の瞬時値pは次のように表される、ここでE、Iを何れも実効値の電圧と電流とする。
| (拡大画面:3KB) |
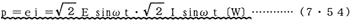 |
これは、抵抗回路であるから、7・4・2(1)で述べたとおりeとiとは同位であるので上式が成り立つ。
また、電力は交流の場合は1周期間のPの大きさの平均値で表されるから、この値を平均電力又はただの電力といっている。
| (拡大画面:13KB) |
 |
|
注:
|
EI cos2ωtの平均は零になる理由は1周期中に2倍の周波数となる。すなわち、+、−、+、−となるため電力は零となる。( 6・1・10の〔応用〕を参照のこと。) |
〔例題〕
(1)100〔V〕の交流電圧で、20〔A〕の電流が流れている電熱器の消費電力〔kW〕を求む。
〔解〕 P=100×20=2,000〔W〕、2〔kW〕
〔例題〕
(2)10〔Ω〕の抵抗に100〔V〕の交流電圧を加えた場合、回路に消費する電力〔W〕を求む。
〔解〕
純粋の容量リアクタンス又は誘導リアクタンスのみの回路の電力は計算によれば何れも零である。よって直列のインピーダンス回路の電力を計算してみる。
図7・48
図7・48(a)のような回路において、交流の瞬時値eとiの式を次のように表す。
この場合、7・4・3(2)で説明したとおり、電流はθ〔rad〕だけ遅れる。
| (拡大画面:12KB) |
 |
このように、7・5・1の抵抗のみの電力と異なりcosθが乗じてある。
θ〔rad〕は電圧と電流の位相差であって、これは遅れているときも進んでいるときもあって、L、C回路には必ず付きまとうものである。図7・49(b)のように斜線の部分が+側にあるものと−側にもある。その分だけ電力が少ないことを意味する。cosθについて後に詳しく説明する。
〔例題〕
| (拡大画面:6KB) |
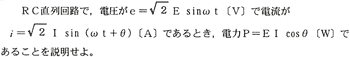 |
〔解〕
| (拡大画面:9KB) |
 |
7・5・1の抵抗のみの回路の電力P=El〔W〕で、直流の場合と同様であるが、7・5・2のインピーダンス回路の電力P=El cosθ〔W〕でcosθが乗じてある。このcosθを電力を表す率という意味で、電力率、略して力率という。英語でPower factor、略してPfと書く。
図7・49
図7・49(a)は、水車の羽根にP点から直角に水があたるときは最も強いが、Q点からθの角度で水があたるときは弱い、これを換言すれば、
OP’=OQ cosθとなる。
即ち、OP−OP'=PP'だけ弱い、
これをベクトルで説明すれば
図7・49(b)は 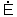 ・ 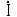 =Pであるが同図(c)ではP= 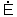 ・ 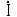
cos 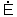 ・ 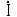 となる。 電圧と電流間に位相差があれば、有効の電力PはE×Iでなく、E×I×cosθとなる。このcosθを力率という意味が理解できると思う。
よって、力率をPfで表せば上式は次のようになる。
| (拡大画面:8KB) |
 |
|