|
6・1・5 特別な角の三角関数
| (拡大画面:20KB) |
 |
| (拡大画面:12KB) |
 |
〔応用〕
| (拡大画面:9KB) |
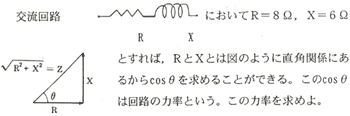 |
〔解〕
| (拡大画面:10KB) |
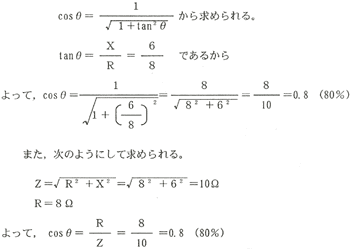 |
| (拡大画面:10KB) |
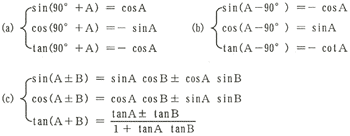 |
|
注:
|
sin(A+B)を代数式のようにsin(A+B)=sinA+sinBと誤解してはならない。
|
| (拡大画面:8KB) |
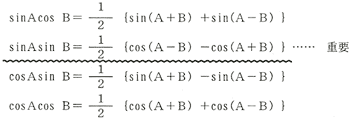 |
〔応用〕
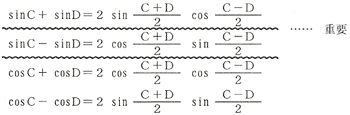
6・1・9 二つの三角関数の和及び差を積の形にする
| (拡大画面:8KB) |
 |
〔応用〕 三相交流の第1相電圧Em sin ωt 第2相電圧Em sin(ωt−120°)のとき線間電圧Elを求める。
sin2A=2 sinA cosA
cos2A=cos2A−sin2A=1−2sin2A=2cos2A−1
一般には、角度を表すには度〔°〕、分〔’〕、秒〔”〕を用いるが電気工学の計算上では弧度(ラジアン、radian)を用い、記号はθで表し単位記号〔rad〕とする。
図6・4
弧度(ラジアン)とは図6・4のような半径1の円(単位円)の円周上を回る点Pの動いた円周上の距離によって角を測る方法である。円弧の長さによって角を測るから弧度という。
そこで半径Iの円の円周=2π・1=2πであるから弧度で測ると360°は2π、180°はπである。これを次のようにかく。
360°=2π〔rad〕 180°=π〔rad〕
よって、
となる。
| (拡大画面:21KB) |
 |
|