|
7・2・3 交流の大きさの表し方
(1)瞬時値と最大値
(2)平均値
| (拡大画面:45KB) |
 |
〔例題〕 最大値Imが10〔A〕の正弦波交流の平均値は何〔A〕か。
〔解〕
(2)実効値
交流の電圧、電流は絶えず変化して、とらえることができない。何らかの形で、その大きさを直流のように表す必要がある、その方法に実効値がある。
これは、次に解析してあるように、ある回路に直流を流した場合の電力量と、同じ回路に同一電力量を得るような交流値を、直流の大きさでいい表せばよいので、この値を実効値という。
図7・9
いま、図7・9(a)において、直流I〔A〕を抵抗R〔Ω〕にT〔S〕時間流せば、
W=R・I2・T〔J〕
また、図7・9(b)において、交流i〔A〕を抵抗R〔Ω〕T〔S〕時間流せば、
W'=(i2の平均)×R×T〔J〕なるジュール熱が発生する。
いま、実効値を得るためには
W=W'でなければならない。
故に、I2R・T=(i2の平均)×R×T〔J〕
よってI2=i2の平均〔A〕
| (拡大画面:22KB) |
 |
Iは電流の実効値を表し、V(又はE)は電圧の実効値を表す。この実効値は、二乗平均値の平方根であるところから、英語では、root mean square value、略してRMSといい、また、effective valueともいう。よってIe、Veと表示する場合もある。
この実効値は広く実用的に使用され、通常は、交流用の電流計・電圧計等は実効値で示されていることに注意しなければならない。
そこで計算によれば( 6・1・10)(〔応用〕を参照のこと。)実効値のI又はVと最大値Im又はVmとの間には次の関係がある。
(4)実効値、最大値、平均値との関連
| (拡大画面:21KB) |
 |
〔例題〕 (1)実効値100〔V〕の交流における最大値及び平均値を求めよ。
(解) 最大値 Vm=100×1.414=141.4〔V〕
平均値 Vav=100×0.9=90〔V〕
〔例題〕 (2)交流電流計の指示が10〔A〕のとき最大値は何アンペアか。
(解) 最大値 Im=10×1.414=14.14〔A〕
今までは正弦波の波形のみについて論じてきたが、交流波形には図7−10に示すようにいろいろあって、これらは数学的に示すには複雑な式が用いられる。ここでは取扱わないことにする。
| (拡大画面:8KB) |
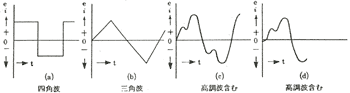 |
図7・10
以上の波形のほかにパルス波形がある。図7・11はこれを示す。
図7・11
|