|
6・1・12 角速度
図6・5
速度は単位時間に物体が変位する割合をいう。例えば、t時間に物体が距離Sだけ動いたときの速度Vは
となる。
これと同様な考え方で、角速度とは、単位時間に回転角の変化の割合を角速度といいω(オメガ)を用い単位記号に〔rad/s〕を用いる。
図6・5において腕rがOを中心としてA点からt秒後に角AOB、即ち、θ〔rad〕回転してB点に達したとすると、角速度ω(オメガ)は
となる。
したがって、ω〔rad/s〕の角速度でt〔s〕秒間回転すれば弧度θ〔rad〕は
θ=ωt・・・(6・3)となる。
〔応用〕
図6・5においてrが1回転すなわち2π〔rad〕だけ回転する時間を周期T〔s〕という。(との意味は何回も回転を繰り返すことから周期という。)
よって(6・2)式は
とかける。
〔例〕
| (拡大画面:7KB) |
 |
いろいろの量の中で、大きさだけでなく、その方向も示さないと、その量を完全に表すことのできない量をベクトル量(以下ベクトルという。)という。そして大きさだけで、その方向を示さない量をスカラ量という。電気工学、殊に交流回路ではベクトルで表す場合が多く、また、その方法が便利な場合がある。
図6・6
図6・6において、ベクトルとはOAのようにその向きとその線の長さOAをもって表す。OBの場合も同様である。そしてベクトルをこのように向きをつけた線分で表す場合には必ず基準線を設けて描くことが必要で、この場合はOxが基準線である。ベクトルの字体は
と書き、その絶対値(方向を除いた値)を表す場合は
と書く。
次に基準線Oxとなす角を偏角といい、Oxから反時計式の方向に回転した角度θ1を正(+)とし、その反対の方向、すなわち時計式方向に回転した角度θ2を負(−)とし、何れも偏角である。
| (拡大画面:5KB) |
 |
注:上記A、Bは絶対値である。
図6・7
図6・7において、図6・7(a)のようにbからaに向って起電力eが発生したとすれば、これをベクトルで表す場合、図6・7(b)のように基準ベクトルとして 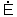 と示す。 次に図6・7(c)のように、aからbに起電力e'が発生したとすれば、これはeとは180°の向きが変わっているので図6・7(d)のように 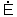 'のベクトルが書けるはずである。ところが方向だけ180°異り、その量が等しければ− 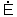 とも書ける。よって 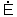 '=− 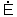 と書いてよいことになる。
| (拡大画面:4KB) |
 |
図6・8
図6・8(a)のように、起電力 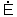 A Aと 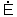 B Bの和は図6・8(b)のように考えられる。よって、このベクトル和を求めるには図6・8(c)、(d)、(e)のように 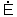 A Aと 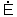 B Bの平行四辺形を画きその対角線がベクトル和となる。即ち、合成起電力Eとなる。 描き方は図6・8(c)、(d)、(e)の何れでもよい。式で書けば
| (拡大画面:10KB) |
 |
図6・9
図6・9(a)において、合成起電力の向きをb 2→a 2にとれば図6・9(b)のように 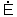 B Bのベクトルは逆になる。この関係即ち 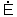 A A+(− 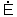 B B)のベクトルを図で画けば図6・9(c)及び(d)のような図になる。図6・9(c)、(d)何れでもよい。よって合成起電力 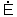 を式で書けば E=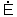 A− A−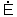 B B・・・ (6・6)となる。
|