|
6・3 複素数によるベクトル表示
図6・10
図6・10において、x軸とy軸の直交座標において  なるベクトルをあらためて考えてみよう。三角関数を使って cosθ=底辺/斜辺=a/A
sinθ=垂線/斜辺=b/A
故に a=A cosθ、b=A sinθ
| (拡大画面:9KB) |
 |
以上の関係から、これだけでは大きさはわかるがその方向は表現できない。ベクトル図法なら大きさと方向の二つの要素を含んでいるから問題はない。そこで、数学的にこれを表現するには複素数を導入する必要がある。複素数について説明すれば次のようである。
図6・11
図6・11において  なるベクトルを数学的に表現するには A=a+jb・・・(6・7)となる。
これを複素数という。
この場合aを実数部、jbを虚数部という。そして、絶対値
である。
(1)jの意義
| (拡大画面:5KB) |
 |
以上述べたように、ベクトルは大きさと方向の二つの要素をもっているので、このjを導入したほうが、電気の理論を解くのに便利であることを1893年頃、アメリカのスタインメッツが発表し現在に至っている。
これは、図6・11のようにx−yの直交軸においてx軸方向を実数、y軸方向を虚数にとる。この虚数にはjを付ける。これによって複素数が完成し、前記のとおり、数学的にベクトルの表示ができる。
図6・12
次にjの性質を考えよう。
図6・12においてjを乗ずることは、
即ち、
| (拡大画面:20KB) |
 |
(2)複数数の絶対値の求め方
(3)共役複素数(共役ベクトル)
a2+b2=(a+jb)(a−jb)式から
(a+jb)と(a−jb)との二つの複素数は互に共役であるという。
これを共役複素数又は共役ベクトルという。
〔例題〕 (1)  =3+j4のZの絶対値Zはいくらか。 〔解〕
〔例題〕 (2) 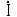 =6+j8〔A〕で表される電流〔I〕を求む。 〔解〕
(1)sin2θ+cos2θ=1 なることを証明せよ。
(2)sinπ/6、sinπ/4、sinπ/3、sinπ/2 それぞれの値はいくらか。
(3)cosπ/6、cosπ/4、cosπ/3、cosπ/2 それぞれの値はいくらか。
(4)弧度について説明せよ。
(5)1〔rad〕は何度に相当するか述べよ。
(6)角速度について説明せよ。
(7)偏角とはどんな角か説明せよ。
(8)ベクトルの和と差を図で説明せよ。
(9)複素数を説明せよ。
(10)jの意義を説明せよ。
(11)複素数の絶対値を示せ。
|