|
6. 電気用数学の手ほどき
| (拡大画面:53KB) |
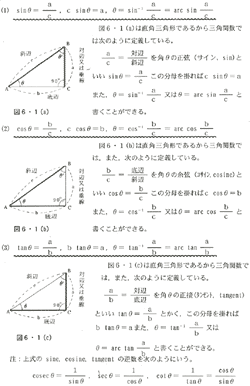 |
図6・1において、 c=1とすれば
6・1・1における式は次のようになる。
| (拡大画面:6KB) |
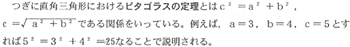 |
ここで、このピタゴラスの定理、すなわち、a2+b2=12を適用すれば
sin2θ+cos2θ=1なる関係式ができる。
注:(sinθ)2をsin2θで表すがsinθ2ではない。sinθ2とかけばθ2の正弦となるので注意を要する。
また、図6・1の角θ'について考えれば
sinθ'=cosθ、cosθ'=sinθ とかける。
また、三角形の内角の和は常に180°であるからθ’=90°−θ
それ故にsin(90°−θ)=cosθ、cos(90°−θ)=sinθの関係が得られる。
図6・2
図6・2において、直角三角形の斜辺cと1角Aが与えられたときは
これらをc倍すればa=c sinA、b=c cosA、となり各辺の長さが求められる。いろいろの角に対するsin、cos、tanの値は数表で求められるから、これを利用してa、bの値が算出される。
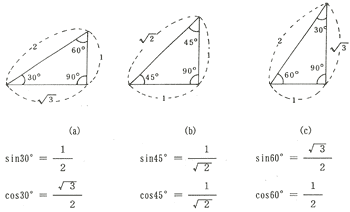
6・1・4 角Aが30°、45°、60°の直角三角形の各辺の数値
| (拡大画面:10KB) |
 |
|
注:
|
2≒1.414 人よ人よ(ヒトヨ、ヒトヨ)と記憶のこと。
|
|
|
3≒1.732 人並みに(ヒトナミニ)と記憶のこと。
|
|