|
4.3 試験成績から外力の影響を修正する方法に関する検討
操縦性試験で得られた操縦性能を表す指標値は、そのままの形で利用できることが望ましいが、試験時の外乱の条件によっては、その影響を除去する必要があるため、外力の影響を修正する方法について検討を行った。
まず、旋回性能における外力の影響修正については、通常、潮流の影響を修正する必要があることから、360°旋回する間の漂流量を利用して旋回航跡を修正する方法が一般に利用されている。この方法の有効性の確認のために、SR221 A、SR221 B船型に対してアドバンスとタクティカルダイアメータについて外乱修正を行った結果を表4.6と表4.7に示すが、旋回初期運動の影響が大きいアドバンスについては、漂流量に基づく修正が逆効果になる場合も見られるが、総じて修正法として利用できると判断される。
続いて、Z試験に対する外乱影響の修正法について検討を行った。Z試験の場合には運動が過渡的であり、旋回試験のような定常的な漂流量を利用するような形の外力影響の除去は難しい。また、簡単な応答方程式を用いた修正の可能性についても検討を行ったが困難であった。従って、数学モデルに外力の影響を考慮したシミュレーション計算による検討を行った。
まず始めに、実船の主要目等から操縦流体力と外力影響を推定した。流体力の推定については、 第6章に示されている長谷川の推定式を用いた。続いて、この運動モデルを用いて、試験時と同様な外力条件下でのZ試験のシミュレーション計算を実施するが、Z試験の推定精度に大きな影響を及ぼす流体力微係数の Y'rの項について調整を行い、第1オーバーシュート角の実船試験結果とシミュレーション計算結果を一致させる。第1オーバーシュート角は針路安定性を表す指標であるから、実船試験結果とシミュレーション計算結果を一致させることにより、数学モデルと実船は針路安定性がほぼ一致しているものと考えられる。最終的に、調整を行った数学モデルを用いて外力影響がない場合のZ試験のシミュレーション計算を行って得られたオーバーシュート角を操縦性能指標の値として採用した。
表4.6 漂流量修正後のアドバンスに対する外乱の影響(風速10.7m/s、波高2.5m)
| 設定外乱 |
風のみ |
波のみ |
風と波 |
| 入射角 |
SR221 A |
SR221 B |
SR221 A |
SR221 B |
SR221 A |
SR221 B |
| −90° |
1.0% |
0.8% |
2.5% |
2.3% |
3.5% |
3.1% |
| −60° |
0.6% |
0.6% |
2.1% |
2.2% |
2.8% |
2.8% |
| −30° |
0.0% |
0.0% |
0.8% |
1.0% |
0.8% |
1.1% |
| 0° |
−0.6% |
−0.5% |
0.1% |
0.5% |
−0.5% |
0.0% |
| 30° |
−1.0% |
−0.8% |
−0.8% |
−0.6% |
−1.7% |
−1.0% |
| 60° |
−1.1% |
−0.9% |
−1.8% |
−1.2% |
−2.9% |
−2.1% |
| 90° |
−0.9% |
−0.8% |
−2.2% |
−1.8% |
−3.1% |
−2.5% |
|
表4.7 漂流量修正後のタクティカルダイアメータに対する外乱の影響(風速10.7m/s、波高2.5m)
| 設定外乱 |
風のみ |
波のみ |
風と波 |
| 入射角 |
SR221 A |
SR221 B |
SR221 A |
SR221 B |
SR221 A |
SR221 B |
| −90° |
−0.3% |
−0.3% |
−0.4% |
−0.3% |
−0.7% |
−0.6% |
| −60° |
−0.2% |
−0.1% |
0.2% |
0.3% |
0.1% |
0.3% |
| −30° |
0.0% |
0.0% |
0.5% |
0.6% |
0.4% |
0.7% |
| 0° |
−0.1% |
−0.1% |
0.5% |
0.7% |
0.4% |
0.6% |
| 30° |
−0.2% |
−0.2% |
0.5% |
0.5% |
0.2% |
0.4% |
| 60° |
−0.2% |
−0.2% |
0.4% |
0.5% |
0.2% |
0.3% |
| 90° |
0.0% |
−0.1% |
0.6% |
0.7% |
0.5% |
0.7% |
|
表4.8に、以上の修正を考慮して行ったシミュレーション計算により得られた結果を示す。また、図4.1にはSR221 A船型に対する舵角と回頭角の時系列を示す。表4.8と図4.1を見ると、拘束模型試験から得られた操縦微係数に基づくシミュレーション計算から得られたオーバーシュート角と長谷川の推定式から得られた操縦微係数を修正した微係数に基づくシミュレーション計算から得られたオーバーシュート角は良く一致していることから、実船試験成績を利用して操縦微係数を修正することにより、無外乱状態におけるオーバーシュート角を推定することが可能となる。
表4.8 Y'rを調整したZ試験のシミュレーション計算結果
| |
実船試験 |
長谷川の推定式 |
長谷川の推定式を修正 |
| Y'β |
0.255 |
0.280 |
| Y'r−m'x |
0.0345 |
0.0185 |
0.0267 |
| N'β |
0.132 |
0.132 |
| N'r |
−0.0463 |
−0.0459 |
| N'β{Y'r−(m'+m'x)}−Y'βN'r |
−0.0223 |
−0.02367 |
−0.0226 |
| 外乱条件 |
外乱 |
無外乱 |
外乱 |
無外乱 |
外乱 |
無外乱 |
| 初期旋回 |
1.71 |
1.74 |
1.69 |
1.72 |
1.70 |
1.73 |
| Ψ1(deg.) |
8.46 |
9.04 |
8.97 |
9.59 |
8.46 |
9.00 |
| Ψ2(deg.) |
22.0 |
24.4 |
23.6 |
26.3 |
21.4 |
23.7 |
|
| |
実船試験 |
長谷川の推定式 |
長谷川の推定式を修正 |
| Y'β |
0.323 |
0.318 |
| Y'r−m'x |
0.0688 |
0.0490 |
0.0593 |
| N'β |
0.114 |
0.114 |
| N'r |
−0.0538 |
−0.0553 |
| N'β{Y'r−(m'+m'x)}−Y'βN'r |
−0.00847 |
−0.0101 |
−0.00899 |
| 外乱条件 |
外乱 |
無外乱 |
外乱 |
無外乱 |
外乱 |
無外乱 |
| 初期旋回 |
1.84 |
1.86 |
1.83 |
1.86 |
1.85 |
1.88 |
| Ψ1(deg.) |
3.57 |
3.63 |
3.73 |
3.80 |
3.57 |
3.63 |
| Ψ2(deg.) |
6.32 |
6.43 |
6.93 |
7.09 |
6.38 |
6.50 |
|
| (拡大画面:20KB) |
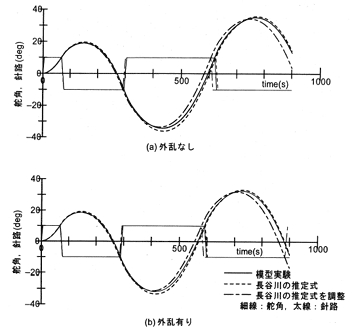 |
図4.1 SR221 A船型のZ試験シミュレーション計算結果
本章に示したZ試験の外力修正法は、微係数の推定がある程度の精度で行われると、有効な方法になる。よく知られた井上の推定式の利用を試みたが、この方法では船尾フレームラインの形状が操縦微係数に及ぼす影響を反映できないため、針路安定性が大きく異なる推定結果が得られることになる。しかしながら、なんらかの方法で微係数を推定し、実船試験成績を利用して微係数に修正を施すことにより、実用的な外力影響の修正を行うことが可能になるであろう。
|