|
3.3 バラスト状態における操縦性能の簡易推定法
操縦性暫定基準の解説書によれば、載貨状態の修正法の一つとして次のような方法が提案されている。
R=T・F/B (3.4)
ここで、
B:試運転状態での推定値(模型試験あるいは理論計算)
F:満載状態での推定値(模型試験あるいは理論計算)
T:試運転状態での計測結果
R:満載状態での操縦性能
このとき、前述の満載状態に対する簡易推定式だけではなく、バラスト状態に対する簡易推定法も必要になるため、ここではその検討結果について示す。
まず、10°/10°Z試験における第1オーバーシュート角ψ10−1、第2オーバーシュート角ψ10−2、20°/20°Z試験における第1オーバーシュート角ψ20−1、10°/10°Z試験において蛇角を10°取ったときに初期方位から10°変針するまでの船舶の船走距離STの推定式は次式のように表される。
| (拡大画面:19KB) |
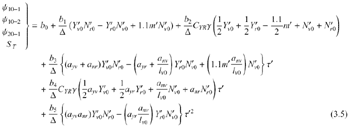 |
また、アドバンスADおよびタクティカルダイアメータTDの推定式については、次式で与えられる。
| (拡大画面:24KB) |
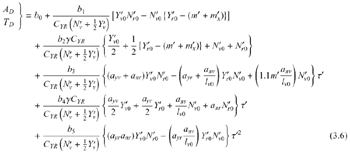 |
ここで、b0〜b6は各性能指標ごとに異なる値をとる係数、Y'ν0'、Y'r0、・・・、l'ν0等に含まれる添字の‘0’は等吃水状態における値であることを示す。また、τ'はトリム量の無次元値、ayν、ayr、anν、anrは操縦微係数に対するトリム修正のための係数である。
バラスト状態に対する実船試験データを利用して求めた(3.5)式および(3.6)式に対する係数を相関係数とともに表3.2に示す。また、推定値と計測値の比較を図3.2に示す。図中の点線は推定値からの標準誤差(Standard Error)の値だけ上下させた値である。図3.2を見ると、10°/10°Zの第2 オーバーシュート角の計測値が15°を越えるものの一致があまり良くないが、全体としては傾向を良くとらえている。
表3.2 バラスト状態における簡易推定法における相関係数および簡易推定式の係数
| Item |
Turning Ability |
Initial Turning Ability |
Course Keeping Ability & Yaw Checking Ability |
| Test |
Turning |
10° / 10° Zig-zag Manoeuvre |
20° / 20° Zig-zag Manoeuvre |
| Index |
Advance / L |
Tactical Diameter / L |
Track Reach / L |
1st Overshoot Angle (deg.) |
2nd Overshoot Angle (deg.) |
1st Overshoot Angle (deg.) |
| Coefficient of Correlation |
0.695 |
0.692 |
0.762 |
0.824 |
0.795 |
0.780 |
| Standard Error |
0.273 |
0.443 |
0.167 |
1.295 |
2.803 |
2.547 |
| Observed Data |
87 |
87 |
84 |
84 |
84 |
82 |
| Number of Parameters |
5 |
5 |
5 |
5 |
5 |
5 |
| b0 |
3.612 |
-0.075 |
2.326 |
12.164 |
23.275 |
26.271 |
| b1 |
1.900 |
5.197 |
0.552 |
4.679 |
6.515 |
10.830 |
| b2 |
-0.343 |
5.610 |
-0.386 |
-2.240 |
-6.317 |
-5.835 |
| b3 |
-6.390 |
-11.723 |
-4.295 |
11.147 |
34.047 |
-21.716 |
| b4 |
-47.651 |
-85.495 |
-8.494 |
-79.533 |
-64.288 |
-307.713 |
| b5 |
-8.768 |
-13.390 |
0.961 |
-36.703 |
-75.130 |
-49.753 |
|
| (拡大画面:74KB) |
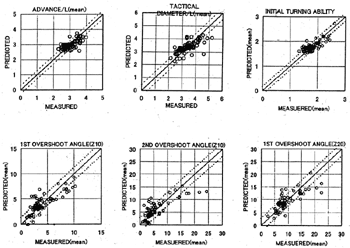 |
図3.2 バラスト状態における実船試験の計測値と推定値の比較
操縦運動の影響を考慮した舵力の項を含む回帰式に基いて、操縦性暫定基準に定められた満載状態における操縦性能指標に対する推定式を作成し、実船の操縦試験結果との比較を行った。その結果、本推定法により船舶の主要寸法や船型を表すいくつかのパラメータを利用して、暫定基準の各指標を推定できることを示した。さらに、バラスト状態に対しても満載状態と同様な手法を適用し、船舶の主要目、吃水、トリム量をパラメータとする操縦性能指標の推定式を作成した。
本章で示した回帰式のパラメータは操縦運動方程式から導出していることから、この考え方は実船の操縦試験データを持つ造船所等で実用的な推定手法として利用できるものと考える。
参照文献
[1]IMO Resolution A.751(18) : Interim Standards for Ship Manoeuvrability, Nov., 1993 [2]平野雅祥他:第3回操縦性シンポジウム、V.造船設計への操縦運動数学モデルの応用II−実船の操縦性能推定−、日本造船学会、1981 [3]Haraguchi, T. : Simple Estimation Method on Ship Manoeuvrability by Means of Manoeuvring Performance Database, Proceedings of MARSIM 2000, May, 2000 |