|
2.1.7 はりの断面寸法の決め方
はりの断面は、そのはりに生じる最大曲げモーメントと、はりの材料の許容曲げ応力とから計算して得たZの値に基づいて決定する。たとえば、50cm3のZが必要であると計算されたとき、断面を円にするならば、
すなわち、径80mmの円となる。
また、正方形とした場合は、
となり、一辺が67mmの正方形となる。材料を経済的に使用するためには、断面係数が大きく、断面積のなるべく小さい断面を選ばなければならない。
次に例題をあげて説明する。
〔例題1〕
第2.17図のような片持ばりの自由端に、500kgfの荷重が作用するとき、許容応力を1,000kgf/cm2、はりの断面は長方形で高さを12cmとすれば、幅はいくらにすればよいか。
(解)
(1)Mmaxを求める。
Mmax=Wl=500×200=100,000kg・cm
(2)Zを求める。
(3)bを求める。
第2.17図
〔例題2〕
第2.18図のような両端支持ばりに、等分布荷重w=5kgf/cmが作用するとき、許容応力を1,000kgf/cm2、はりの断面を正方形とすれば、一辺の長をいくらにすればよいか。
(解)
(1)反力RA、RBを求める
(2)最大曲げモーメントMmaxを求める。
(3)断面係数Zを求める
(4)正方形断面のZの式を変形してhを求める。
第2.18図
2.1.8 はりのたわみ
はりに荷重が働くと曲げモーメントにより曲げられる。はりが曲がれば各断面はもとの位置から荷重の方向に多少移動する。その移動距離をたわみという。はりは強さの点で十分であっても、たわみが多過ぎると種々不都合なことを生ずる。
計算の結果によると、はりの最大たわみ量ymaxは、一般に次の式で表わされる。
この式で、lははりを支える二つの点の間の距離で、これをスパンという。また、EI(Eは材料のヤング係数、Iは断面二次モーメント)は曲がりに対する抵抗の程度を示すもので、曲げ剛性という。またWははりに働く荷重であり、第2.19図の(a)、(c)、(e)のように、はりの上の一点に集中してかかる荷重を集中荷重といい、(b)、(d)、(f)のように、はりに沿って一様に横たわっている場合を等分布荷重という。
また、はりの両端の支え方は、第2.19図(a)、(b)のような支え方を支持端といって、はりは荷重によって自由な形をとることができる。これに対して(c)、(d)あるいは(e)、(f)の左端のように、末端をしっかりと押さえつけるような支え方を固定端といって、はりは末端では荷重がかかっても動くことができない。また、(e)、(f)のはりの右端のようなものを自由端という。
(8)式のcは、これらの条件により異なる定数で、主なはりのcの値の例を第2.19図に示してある。
船体の構造部材は、弾性があるので、完全な固定端にはならないが、丈夫な大型のブラケットを使えば、固定端に近い状態が得られ、またビームのスパンが実質的に短くなる。また、荷重は、船の場合は、分布荷重が大部分であるが、集中荷重と考えて計算してもよい場合もある。
| (拡大画面:33KB) |
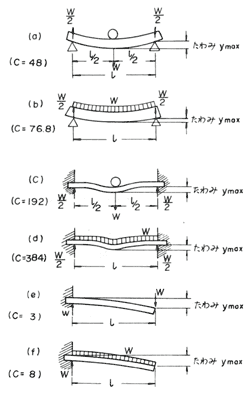 |
第2.19図
|