|
2.1.6 はりの応力
はりに荷重が働くと、せん断力や曲げモーメントが作用する。このとき、はりにはせん断力に対してせん断応力、曲げモーメントに対して曲げ応力が生じてつりあう。この応力がはりの材料の許容応力以内にあれは安全であるが、許容応力を越えると危険である。そこで、はりの断面の形や大きさを適当に決めて、材料内に生じる応力を許容応力以内におさえたり、より強い材料を使って安全にする。そのためには、はりの内部に生じる応力の大きさが、断面の形や荷重のかかり方によってどのようになるか調べてみなけばならない。
(1)はりに生じる応力
いま、第2.11図(a)のようなはりを考え、はりを任意の断面XXで切り、A部とB部とに分けて考える。
第2.11図
B部について考えれば、第2.11図(b)のように、断面XXには外力による曲げモーメントMに大きさ等しく、反対向きの曲げモーメントMr、W2とR2との差に等しいせん断力Fが生じてつり合いを保っている。また、断面XXの左側A部のつり合いもこれと同様で図(c)のようになる。
Mrは曲げモーメントに抵抗するために、この断面に生じたモーメントであるから、これを抵抗モーメントという。抵抗モーメントは、この断面に生じる垂直応力(前に述べた曲げ応力)よって起こるものと考えられる。
一般に、深さに比べて長さの長いはりの強さは主として垂直応力によって定まるものであるから、せん断応力の影響は、長さに比べて深さの大きい場合、その他の特別の場合以外は考えなくてもよい。
(2)断面二次モーメントと断面係数
外力による曲げモーメントとつり合う抵抗モーメントは、断面の曲げ応力Sbによって生じるものである。
第2.12図において、はりのある断面XXの中立軸よりy1の距離に微小面積a1を想像し、このa1上に生ずる応力をS1とすれば、S1上の全応力=S1・a1となり、この全応力の中立軸についてのモーメント△Mは、△M=S1・a1・y1となる。
第2.12図
しかるに、中立軸から最外方までの距離をy、その応力をSbとすればS1=Sb・Y1/Yなる関係がある。この関係を△Mの式に入れて、全体の応力について△Mの総和を求めると、これが抵抗モーメントMrとなり、曲げモーメントMと等しくならなければならない。
| (拡大画面:3KB) |
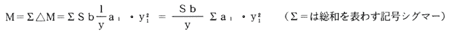 |
上式でa1・yは微小面積a1と、中立軸からその面積までの距離の2乗との積を断面全部にわたって求めた総和で、断面の形状によって定まった値をもつから、普通Iの記号で示し、これを断面2次モーメントという。
Iを用いて上式を書かえると、M=Sb/y・I (8)
となる。
この式の曲げ応力Sbを分析して引張応力St、圧縮応力Scで示し、Stの生じる側のyをyt、Scの生じる側のyをycで表わすと、
式中のI/ytおよびI/ycをそれぞれZt、Zcで示すと、
M=St・Zt、M=Sc・Zc
Zt・Zcは中立軸に関して対象な断面では等しくなるが、これをまとめてZで示すと、
M=Sb・Z または Sb=M/Z (9)
が得られる。このZを断面係数といい、断面の形によって定まる値である。非対称な断面ではそれぞれ異なった二つの断面係数Zt、Zcがある。
(9)式は、はりの設計に最も重要な公式で、式中Sbが材料の許容曲げ応力以下となるように、はりの寸法を決めなければならない。
次に、はりの経済的な形を考えてみよう。
式M=Sb・Zにおいて、Mが一定ならばZが大きいほどSbは小さくなるから、はりは丈夫になる。またSbが一定でZが大きければ、大きな曲げモーメントに耐えられることになる。いずれにしてもZを大きくすればよいわけである。断面積を大きくすればZは大きくなるがそれでは不経済である。
そこでZを表わす一般式を考えてみると、
で示されるから、この式でyが一定ならばIが大きいほどZを大きくすることができる。しかるにI=Σa1・y12であるから同じ断面積a1の材料であっても、中立軸からの距離y1を大きくすれば、距離の2条に比例してIを大きくすることができることがわかる。したがってy1とa1とを一定とした場合、中立軸に遠い位置に多くの面積を有するような断面の形をつくれば丈夫なわけである。
このことは、第2.13図に示す4種類の断面形状を持つはりについて考えてみても明らかなことである。このはりの断面がどれも同じ面積で、長さを一定とすれば重さが同じであるが、曲げモーメントに対する強さを比較してみると、
となり、中立軸に最も遠い位置に面積を多く持っているDの形状が強いことがわかる。
| (拡大画面:12KB) |
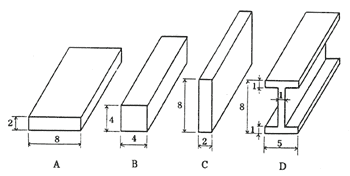 |
第2.13図
この考え方をさらに進めて、船全体を一つの中空のはりと考えれば、その中立軸から遠い上甲板・舷側厚板・キール・船底外板・縁板などを厚くすることが、船の強度を増すのに非常に有効であることがわかるであろう。
(3)各種断面の断面係数
各種断面の断面係数を求めるには、まず中立軸の位置を定め、中立軸に対する断面二次モーメントの値を求める必要がある。これが求まれば、断面二次モーメントIを中立軸から断面の最外方までの距離yで割って、断面係数Z=I/yが求められる。簡単な断面(長方形と円形)の断面二次モーメントと断面係数の値を第2.14図に示す。
| (拡大画面:19KB) |
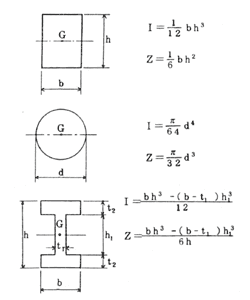 |
簡単な断面の断面二次モーメントと断面係数
第2.14図
第2.15図に示すように、中立軸(x軸)は必ず断面の重心Gを通る。中立軸(x軸)に対する断面二次モーメントをI、中立軸に平行なx'軸に対する断面二次モーメントI'とすれば、
I'=I+ 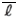 2 2・A (10) なる関係がある。ただし、 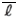 は中立軸x軸とx'軸との距離、Aは断面の面積である。
第2.15図
(10)式により重心を通らない任意の軸に対する断面二次モーメントを求めることができる。
(10)式と第2.14図のような簡単な図形の断面二次モーメントを用いて、種々の複雑な断面の断面二次モーメントを計算することができる。それには断面の中立軸の位置をあらかじめ仮定し、断面を形成する各部材の仮定中立軸に対するIを(10)式により計算してこれらを加え合わせて、仮定中立軸に対する断面二次モーメントI'を求める。次に全断面の重心を通る真の中立軸と仮定中立軸との距離を求め、再び(10)式により真の中立軸に対する断面二次モーメントIを求める。
以下に具体的例として、板付平鋼についてI、Zの求め方を説明する。
| (拡大画面:14KB) |
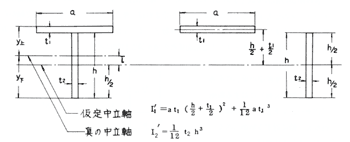 |
第2.16図 板付平鋼
| (拡大画面:21KB) |
 |
実際には各種の板付形鋼(平鋼、山形鋼、逆山形鋼、不等辺不等厚逆山形鋼、球山形鋼、球平形鋼、溝形鋼)の種々の寸法のものについて、断面係数、断面二次モーメントの値を与える表があるので( 学習指導書末尾の附表を参照すること)これを利用すると便利である。船体のような複雑な断面については、各部材についていちいち上のような計算を行なうので、表をつくって計算するのが普通である。 |