|
7. 主要構造部材寸法の計算に対する各構造基準の考え方
7.1 梁理論
船体は皮材と骨材で構成される剛な梁(Beam)と見なし、その基本的外力である曲げに対する強度は梁理論(Beam Theory)に基づいて計算される。船体局部を構成する骨材も同じく梁理論で計算される(座屈に対しては座屈理論による。皮材も別途理論による)。
梁理論では、曲げ荷重による船体各部の曲げ応力σは次式で求められる。
| σ=M/z |
M:部材に働く曲げモーメント |
| |
z:部材の断面係数 |
従って、もしσ=許容応力=一定とすれば、zはMに比例して増減しなければならない。
梁ではその両端の固着条件(両端固定、一端固定他端支持、両端支持等)や荷重形態(集中荷重、分布荷重等)並びに着力点の変化等により部材の各位置での曲げモーメントの値は変動する。
参考までに図7−1に代表ケースについてのそれらの関係を示す。アルミ合金船の構造基準類では、各骨部材に対し殆ど全てこれらの何れかのケースをその構造条件に応じて適用している。
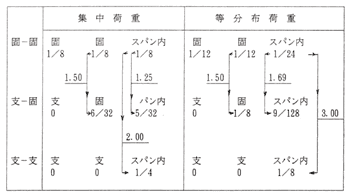
図7−1 により、固着条件の差違による梁の各位置における曲げモーメントの値を比較してみると図7−2 のようになる。部材端取合い部の設計においては、この固着条件差による曲げモーメントの変動量を十分理解して置かねばならない。
図7−1 代表的な梁の曲げ特性比較
| (拡大画面:37KB) |
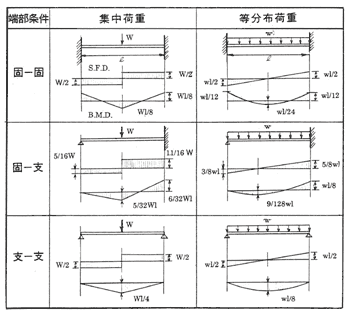 |
図7−2 端部固着条件差による曲げモーメント値の変動(係数比較)
| (拡大画面:19KB) |
 |
7.2 断面係数
7.2.1 弾性設計と塑性設計
昭和47年に制定された軽構造船暫定基準は、当時の構造設計思想の影響もあり、塑性設計概念に基づいて作られたが、その後の各基準類は全て通常の弾性設計概念に戻って作られている。
金属材料の応力−歪曲線を単純モデル化すると、下図のように応力と歪が比例する領域(弾性領域)と応力値は殆ど変わらないのに歪が増加する領域(塑性領域)とに区分される。
梁に曲げモーメントが作用する場合、梁の上下外皮での応力が最大となる。
弾性設計の場合、この上下外皮での応力が弾性領域の限界である降伏点(耐力)に到達するのを限度として設計する。従って梁の内部は弾性を保持したままである。
これに対し塑性設計の場合は、上下外皮の応力が降伏点(耐力)を超えた後も、断面全てが塑性変形するまでは抵抗力があるとする。
このように両概念には開きがあるが、概念の違いにより実船の部材に大きな乖離を生じても困るので、例えば軽構造船暫定基準の後に作られた軽構造船構造基準(案)(RR11)では荷重条件を調整して両者の整合を計っている。
7.2.2 弾性設計及び塑性設計の断面係数
弾性設計での断面係数Zは次のように定義される。塑性設計の断面係数ZPは下図に示すようにこれとは異なる。
| Z=I/y |
I:断面二次モーメント |
| |
y:中性軸から最外皮までの距離 |
矩形断面について弾性断面係数z、塑性断面係数zPpを比較すると次の通り。
●Z=(1/2・b・h/2)・(h/2・2/3)× 2
=bh2/6
●ZP
=(b・h/2)・h/4 × 2=bh2/4
●ZP/Z=1・5・・・形状係数
7.2.3 断面係数の計算法
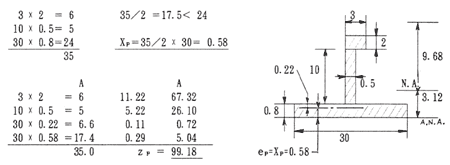
(1)塑性断面係数
代表例を示す。形状が異なる場合もこれに倣う。
●(bOtO+h1t1+bt2)/2<bOtOの場合
XP=(bOtO+h1t1+bt2)/2b0
ZP1=(t0−XP+h1+t2/2)bt2
ZP2=(t0−XP+h1/2)h1t1
ZP3=(t0−XP)xb0x(t0−XP)/2
ZP4=XPxb0xXP/2
ZP=ZP1+ZP2+ZP3+Z1P4
●(b0t0+h1t1+bt2)/2>b0t0の場合
ZP=b0t0/2(h1+t0)+bt2h/2+h12t1/4−1/4t1(bt2−b0t0)2
●塑性断面係数計算例
(bOtO+h1t1+bt2)/2<bOtOの場合
| (拡大画面:18KB) |
 |
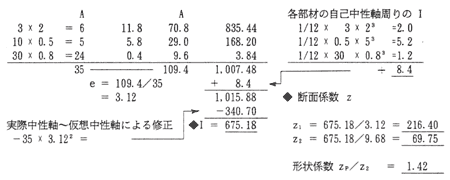
●弾性断面係数計算例(同上図による)
板下面を仮想中性軸(A.N.A.)として計算。
| (拡大画面:21KB) |
 |
|