|
TIDAL SIMULATION IN ARIAKE SEA BY PARALLELIZED OCEAN MODEL
Kyeong Ok Kim1 and Takao Yamashita2
1Department of Civil Engineering, Kyoto University Uji, Kyoto, JAPAN
kokim@rcde.dpri.kyoto-u.ac.jp
2Research Center for Disaster Environment, Disaster Prevention Research Institute
Uji, Kyoto, JAPAN
ABSTRACT
The tide of the Ariake Sea is characterized by very large difference of tidal height and strong tidal current. In recent years, the Ariake Sea has encountered serious environmental problems, typified by the seaweed damage, which may be caused by serious proliferation of phytoplankton due to environmental changes, such as tidal transformation by coastal development. In this study, characteristics of the tide and tidal current in the Ariake Sea were investigated with the numerical experiment by a parallel three-dimensional primitive σ-coordinate model for seawater circulation. The parallel linux system was used to calculate and predict the Ariake Sea tide. The computed results were compared with the existing charts and coastal tidal observations. The influence of Isahaya Dike on the changes in tidal environment in the Ariake Sea was also examined.
INTRODUCTION
The Ariake Sea is a large bay and macro-tidal estuary located in the western part of Kyushu Island, the southwestern part of Japan (Fig.1). This sea is the main production area of "Nori"(seaweed) in Japan, providing nearly half of the nations supply. In the recent years, environmental factors have changed in the Ariake Sea; turbid sea water, increased sea water level, changed fish species, risen sea water temperature, etc. The Ariake Sea has suffered a general deterioration of its environment, impacting the general economy of the region and especially leading to dramatic seaweed crop failures caused by unusual red tides. Lots of aggravation factors can be included on this issue; decrease of tideland area, development of coastal industrial area, water pollution, etc. But it is still not clear in detail because of its complexity. In 1952, looking at ways to boost rice production after the War and to solve food shortage problems, decided to drain parts of Isahaya Bay. The construction of Isahaya Dike was started in 1988 and the bay was closed by a 7 km-seawall constructed by the Ministry of Agriculture, Forestry and Fishery on April 14, 1997. A possibility of a negative effect of this reclamation project on seaweed harvests in the Ariake Sea becomes the target of debate of physical-biological relation.
In this research, characteristics tide and tidal current, one of the most important
physical factors, in the Ariake Sea and the effect of seawall construction in Isahaya Bay were investigated
by numerical experiment using the parallel three-dimensional primitive σ-coordinate model in the Linux-based
parallel clustering computer system which connected four clients together via 100M based Ethernet (Fig.2).
This code came from the TOPAZ project at the University of Minnesota. TOPAZ is a compiler tool that helps
in the conversion of serial codes to parallel form. TOPAZ was used to help create a parallel version of
the POM97 code. ( Oberpriller et. al., 1998)
Figure 1. The water depth chart of the computational domain and the location
of the Ariake Sea, Isahaya Bay and the tidal observation stations
Figure 2. Linux-based parallel clustering computer system
NUMERICAL MODEL
The basic equations consisting of the continuity, momentum, hydrostatic, temperature, salinity and density equations of the three-dimensional primitive σ-coordinate model are given by
| ux+vy+wz=0 (1) |
| ut+uuxvuy+wuz-fv=-ρ0-1px+(KMuz)z+Fu (2) |
| vt+uuxvvy+wvz+fu=-ρ0-1py+(KMvz)z+Fv (3) |
| ρg=-Pz (4) |
| θt+uθx+vθy+wθz=(KHθz)+FT (5) |
| ρ=ρ(θ) (6) |
where ( u,v,w) are the velocity components in the ( x,y,z) directions,
respectively, p the pressure, θ the temperature or the salinity, ρ in situ density,
ρ0 (=const.) the reference density, f the Coriolis parameter,
g the acceleration due to gravity, KM the vertical eddy viscosity,
K H the vertical eddy diffusivity, F(u,v) the
horizontal eddy friction terms, and F(T,S) the horizontal eddy diffusion
terms. The KM and KH are determined
by Mellor and Yamada level 2.5 turbulence closure model ( Mellor and Yamada, 1982).
The horizontal friction and diffusion terms are given by Smagorinsky nonlinear viscosity. The model first
transforms (1)-(6) into the sigma coordinate system defined by σ=(z-η)/(H-η) where η and H
are the surface elevation and the water depth, respectively. The resulting equations are splitted into
the external (vertically averaged) and the internal (3-D) modes, and they are solved by the mode splitting
method, an idea originally developed by Simons (1980). The Asselin filter
is used every time step to prevent a split in the solution associated with the leapfrog scheme. The hybrid
friction is hired for calculation of bottom friction. ( Luettich and Westerink,
2000)
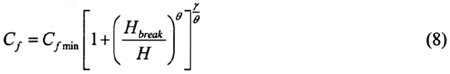
In the hybrid friction relationship Cf approaches Cf min in deep water (H > Hbreak ) and approaches Cf min (Hbreak| H )γ in shallow water(H < Hbreak ). The value of Cf min is 0.0025, Hbreak is 20, θ is 1/3, γ is 1. In this study area, Cf is distributed in 0.0025〜0.0045.
The model computed by the horizontal grid size of 30 arc-second (about 900
m) and the external and internal time step of 0.5 and 15 seconds. The water depth data was composed by
digitized numerical data from sea maps and 1-minute grid digital East Asia topographic data from Sungkyunkwan
University ( Choi et. al., 2002). The tidal elevation in open boundary was interpolated
by the observed data at Sasebo and Akune, and modified to improve the reappearance of tide in the Ariake
Sea. |