4.8 境界条件
4.8.1 側面境界条件
側面境界に直行する風速成分およびその他の変数の側面境界条件は
で与える。ここでnは側面境界条件に直行する座標軸で、添え字rは初期値となる
データを意味する。
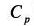
はひとつ内側の格子点で求められる
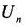
の位相速度である。
位相速度Cqは北と東境界では正、南と西境界では負で、その絶対値は30m/sとする。
緩和係数γは1/3600s
-1とする。
上部境界では
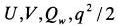
の鉛直勾配は0とし、
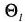
の勾配は初期値に固定する。上部境界からの重力波の反射を抑えるために、
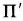
の上部境界値はKlemp and Durran(1983)が提案した鉛直風速Wとの関係式
で与える。ここでハットはFourier成分を現す。Nはブラントーバイサラ振動数、k
および1は格子構造に依存するX方向およびy方向の波数である。
4.9 数値解法
数値計算は、領域を多数の格子で分割し、微分を差分で近似して解く格子法
により行う。鉛直および水平断面の格子構造を下図に示す。
鉛直風速
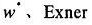
関数
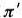
および鉛直拡散係数
は、
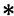
印の位置で定義し、水平風速
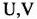
乱流エネルギー
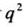
、温位
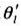
、比湿qwやそのほかのスカラー量は、○印の位置で定義するスタッガード格子系である。
また乱流エネルギー
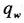
は正の値でなければならないので、その移流項の差分には上流差分を用いる。その他の空間差分は2次の精度の中央差分で近似する。時間積分におけるタイムステップは、CFL不安定を回避するように設定しAltenating Direction Implicit(ADI法)を用いて行う。ただし雨滴の落下速度は大きいので降水過程はbox-Lagrangianスキームで行う。
次ページにADI法について記述する。
座標系における物理量
の方程式を以下のように表す。
