4.4.2 太陽放射
大気上端に入社した太陽放射は、地表面に到達するまでに、大気中の空気分子、
水蒸気やエアロゾルによって散乱や吸収を受けて減衰する。そこで、波長に応じて
散乱部分と吸収部分の2つに分離して散乱・吸収を計算する。オゾンやエアロゾル
の効果を無視すると、散乱部分はRayleigh散乱と雲水による反射だけを扱えばよい。
一方、吸収部分は水蒸気と雲水による吸収、雲水による反射からなっている。
日射を分離する波長は、0.9μm(Katayama,1972)ではなく0.75μm(Stephens,1978)
を採用する。散乱部分のRayleigh散乱による反射率は、Katayamaの式で見積もり、
吸収部分の水蒸気による吸収率は、Lacis and Hansen(1974)の式で求める。
雲水による反射率と透過率は、Stephens(1978)とStephens et al(1984)にしたがっ
てパラメタライズする。多重層では、これらを2方向放射伝達モデル(たとえば、
Chen and Cotton,1983)を利用する。ただし、ここでは下からの反射を無視するため、
散乱光の吸収などは考慮しない。したがって散乱は地表面についてのみ扱う。
直達光の太陽放射量
散乱・吸収は、簡単のため太陽放射を可視域
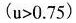
と近赤外域
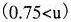
に分離して扱う。
・可視域
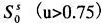
空気分子によるレイリー散乱・・・(ii)
雲による反射・・・・・・・・・・・・・・・・(iii)
・近赤外域
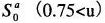
水蒸気による吸収・・・・・・・・・・・・(i)
雲による反射・吸収・・・・・・・・・・・(iii)
(i)水蒸気による吸収
散乱吸収関数はManabe and Meller(1961)にしたがって
吸収量(absorptance)
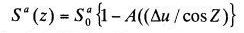 |
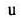 : 光学的厚さ : 光学的厚さ |
(ii)空気分子によるレイリー散乱
レイリー散乱によって散乱された放射は大気中では吸収されない。したがって地表面のみで扱う。
散乱率
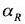
(albedo)
地表面に達する散乱部分は
(iii)雲による反射・吸収
雲による反射・吸収はStephens(1978)のパラメタリゼーションに従った。しかし、Stephensは可視域と近赤外域との分界波長を0.75としいるのに対し、Katayamaは0.9で扱っている。ANEMOSではその違いを無視している。
また、雲による吸収は多重散乱を考慮しなければならない。この概念図を次ページの図に示す。
可視域、近赤外域における特定層における反射率と吸収率は以下の式で求める。
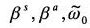
はStephen et al.(1984)のパラメーターを使用している。
可視域
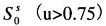
多重散乱を考慮すると、(
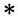
は上向き、
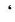
はk層のみの透過・吸収)
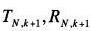
はその層の雲を考慮して下式で表される。
(
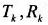
はStephenの近似式から求められるもの)
したがって、トータルの透過率および反射率は次式で表される。
高度
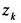
における吸収部分
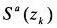
は
ただし、高度
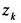
における透過率
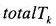
は、第(k+1)層界面を上方に反射するものを除かなければならない。よって次式で表される。
以上から正味の太陽放射吸収量
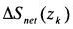
は
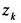
: 上空の場合(散乱による吸収は無視できる)
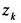
: 地表の場合