電極で電流の涌き出しがあるので、溶液中、の電位φは次のPoisson方程式を満足する。

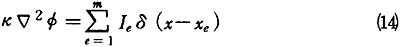
ここでは、I_eは電極eの電流量、δ(・)はデルタ関数、x_eは電極eの位置である。境界条件は式(2)〜(4)で与えられる(ただし、ここでは金属表面をΓ_mで表す)。金属表面Γ_mが防食状態にあるためには、(式(4)が満足されなければならないのと同時に)、次式のように電位を防食電位E_p以下に保つ必要がある。

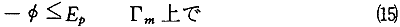
防食を達成するのに必要な外部電力Pは、次式で与えられる。

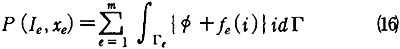
ここで、Γ_e、はx_eを中心とした半径ε(εはΩに比べて充分小さい)の球とする。また、f_e(i)は電極eの分極曲線を表す。

　

5.2　最適化方法

電力最小の条件を最適条件と考えて、式(16)を最適化のための目的関数とする。以上よりカソード防食最適化問題は、式(14)〜(15)および境界条件(2)〜(4)を満足し、式(16)を最小とするI_eおよびx_e(e=1〜m)を求める問題に帰着される。

式(14)を境界要素法により離散化し、境界条件(2)〜(4)を代入した式と防食条件式(15)を満足するI_eおよびx_cの組を求め、その中から電力(16)を最小にするものを探せば最適解を得ることができる。そこで、式(15)を(16)の最小化に対する制約条件と考え、ペナルティ係数κ(大きな正数)を用いて⁷⁾、次式の目的関数を定義する。⁸⁾

P^*(I_e, x_e)=P(I_e, x_e)+κ‖b((I_ex_e)‖²　(17)

ここで、‖・‖²は2乗ノルムを表し、bは次式で定義される成分からなるベクトルである。

b^j=(φ_j+E_p)H(-φ_j-E_p)　(18)

ただし、H(・)は単位ステップ関数である。

式(17)は式(15)の制約条件が破られると大きな値(ペナルティ)が電力値Pに加算されるように作られている。Pは、適当なI_eおよびx_eを与えてφおよびiを求めた後、電極上の電位φの値を内点の式より求め、式(16)に代入することにより計算される。P^*の最小化には共役勾配法などの繰返し法を用いる。境界要素法では、繰返し計算における電極位置x_eの変更が容易となる。

　

5.3　複雑構造物に対する最適化の工夫

上述の方法で簡単なカソード防食最適化問題を解くことができる。しかし、実際の複雑な問題に対しては、境界要素法を用いても計算量が膨大となるので、この低減が重要な課題となる。そので、以下に示すような様々な工夫が提案されている。²⁾

最小化の計算において、設計変数I_e1およびx_eに対する目的関数P^*の感度解析(微分)が必要となり、3次元問題ではこの計算量が膨大となる。そこで、各境界要素毎に局所座標を導入し、ガウスの発散定理を利用して、大部分の微分を解析的に行う。この方法により計算量の大幅な低減が可能となる。

電極の数が多いと、目的関数P^*が多峰性(多くの極小点)をもつ場合がしばしば現れる。このような問題に対して、共役勾配法やNewton-Raphson法のような降下法を適用するとすれば、異なったいくつかの初期値から検索を行い、それぞれの計算から得られた解を比較して最適解を探すという作業が必要となる。さらに、得られた解が最適であることを保証するために、初期値の数を多くし、なおかつ広く分散させる必要がある。また、降下法では変数の数が多くなるにつれて、勾配を求めるためなどの計算量が膨大になる可能性もある。

そのような最適化問題に対して、遺伝的アルゴリズム(Genetic Algorithms、以下GA)が注目を集めている。しかし、GAは大域収束性に優れているが局所収束には時間がかかるという特徴があり、厳密な正解を得るためにはかなりの計算時間を必要とする。そこで、GAにクラスタリングと降下法を組み合わせることで、より効率的に最適化を行う手法が開発され、カソード防食の最適化問題に応用されている。⁹⁾

前ページ　　　目次へ　　　次ページ