図5　ポンプ表面上における電位分布

　

4.　腐食速度の逆問題解析

前節までは、金属の分極特性を既知として、金属表面上の電位または電流密度(腐食速度)分布を予測するという、いわゆる順問題の境界要素解析手法について述べた。これに対して、例えば、地中埋設構造物に付加した犠牲陽極の有効範囲や寿命を調べたいが、地中における構造物の金属部材や犠牲陽極の分極の分極特性についてのデータがないというような場合も少なくない。土を埋設構造物の所まで掘れば、その構造物の表面における電位を測定できるが、多大な労力が必要となる。地中(できれば地表)の電位の測定値から腐食速度を推定するという、いわゆる逆問題が解ければ好都合である。以下では、このような場合の取扱いについて述べる。なお、逆解析を利用して分極測定の精度を向上させる研究も進められている。²⁾

　

4.1　解析手法

本節では、腐食速度を推定する逆問題解析に対してあいまいな先験情報を利用する手法について考える。図6に示すような外部電源(防食用電源)から船舶外板に電流を流したときの船舶外板表面のセンサー位置での電位の測定値から、分極特性に関する先験情報を利用して、船舶外板各部の電位分布を求める場合がその例である。

従来の逆解析手法では測定点の数が少ないのでこの問題を解くことができないし、測定点の数を増加させても、解が振動してしまって、意味のある推定を行うことができない。²⁾そこで、

　

図6　電極とセンサーの位置

　

金属表面上のφとiは分極曲線を満足するという条件(先験情報)を利用することで、適切な推定を行う。

分極曲線が既知であれば、前節で述べた方法で電流密度を解析し、腐食速度を推定することが可能となる。したがって、腐食速度を推定する逆問題は分極曲線を推定する問題に帰着させることができる。そこで、まず、次式のように、分極曲線を、例えばTafelの式¹⁾などのような数個のパラメータ(α_j)を持った関数で近似する。

φm=-f_m(i_m;α_j)金属表面Γ_m上で　(10)

このようにすることで、逆問題は、パラメータ推定問題となる。

上式を用いると式(6)は

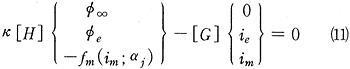
のように書くことができる。ただし、φ_∞は、外部領域問題を解析する場合に必要となる無限遠における電位を表す。

つぎに、α_jの推定を行うために、次式のような目的関数cost(α_j)を定義する。

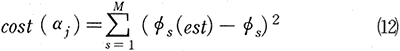
ここで、φ_s(est)は、α_jの推定値を用いて順問題解析、すなわち式(11)を解くことによって得られる電極位置における電位の解析値であり、φ_sは測定値である。関数cost()が測定誤差値ε以下になるまで共役勾配法などでパラメータを補正し、繰返し計算を行えば、原理的には適切なα_jの値を推定することができる。しかし、本問題は少ない測定点を基にして推定を行うので、一般に悪条件となる。すなわち、実際には関数cost()が測定誤差値ε以下になる領域(IIとする)が広く、解を絞り込むことができないという問題点がある。

前ページ　　　目次へ　　　次ページ