(4・4)式はEX−ORの性質から

D³X＋DX＋IX＝0　(4・6)

と書き直せるのでXでまとめると

X(D³＋D＋I)＝0　(4.7)

X・f(D)＝0、ここで、f(D)＝D³＋D＋I　(4・8)

f(D)は符号発生器の伝達関数と呼ばれ遅延単位Dの多項式で表せる。

(4・8)式において、X≠0から符号発生の条件は伝達関数f(D)＝0、となる。

f(D)＝0又はD³＋D＋I＝0　(4・9)

(4・9)式は(4・4)式の右辺を左辺へ移項したものと同じなので現在の符号IXは3ビット遅延したD³Xと1ビット遅延したDXとをEX−OR演算したものに等しいことを示している。

一般に遅延素子Dにシフトレジスタ電子回路が用いられる。シフトレジスタに初期条件を入れるとそれに対応した符号Xが発生される。図4・2の回路で3つのDの初期条件を左端D＝0、2段目D＝0、3段目(右端)D＝1、すなわち

(　0　0　1　)

にセットしたとき発生する符合Xは

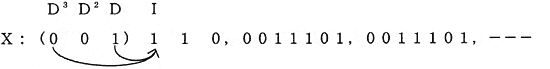
となりXは長さ(周期)7ビットの、(0011101)符号を発生する。

遅延回路からEX−ORへ取り出す端子の組合せにより異なる2元符号を発生できる。n個の遅延回路から取り出せる組合せは2ⁿ通りあるが、すべてが0となる符号を除くと2ⁿ−1、通りの符号が発生できる。この中で最も長い符号をM系列符号と呼ぶ。M系列符号は雑音と似た性質があるので、擬似雑音(PNコード)と呼ばれる。符号化レーダやGPSによる測位にPNコードが使用されている。PNコードは雑音や妨害に強いので携帯電話の符号分割多元接続(CDMA)方式にも使用されている。

前ページ　　　目次へ　　　次ページ