Thus, judging from these theoretical results obtained from Model A and Model B, we can get such important results as the following:

T_va =T_vb / (1-p) + T_e

T_wb = T_d / P +(1/p - 1) T_e　(8)

　

Thus, in spite of Model A or Model B, we prove that T_va = T_vb = T_v, and more T_wa = T_wb = T_w are always held in the case of the exponential distribution.

First, the characteristics of failure maintenance T_v are as follows:

1] In case of p=0, T_v is same form as the basic maintenance model. That is, it is very natural that the results without the diagnosis are equivalent to the basic maintenance model.

2] As p is near to 1, the first term of eq.(6) becomes very large and therefore, T_w is very large. That is, as p increases, the expected interval of CM becomes very large, and the number of PM decreases.

On the other hand, the expected interval of PM T_w has the following characteristics:

3] As p is close to zero, 1/p is increasing, and then T_w is increasing. This fact shows that the expected interval of PM is increasing, and on the contrary, its number is decreasing because of failure of diagnosis.

4] When p is near to 1, the second term of eq.(6) is zero, and T_d is approaching to T_w. That is, when the diagnosis ratio is very high, it shows that the expected interval of PM is equivalent to the expected interval of fault occurrence.

　

3. ANALYSIS AND EVALUATION DUE TO DIAGNOSIS SUCCESS RATIO p

　

In this section, we describe the relation between the expected interval of CM and the expected interval of PM using the results obtained and α = T_m / T_e already introduced [2]. Moreover, from the viewpoints of the number and the cost of maintenance and the improvement of system reliability, the characteristics of relations obtained newly are investigated in detail, and based on these properties some new evaluation methods for the diagnosis based maintenance are proposed [6].

　

3.1 Relation between expected interval of PM T_w and CM T_v

Representing T_w and T_v by α, we can obtain the following relation:

　

　

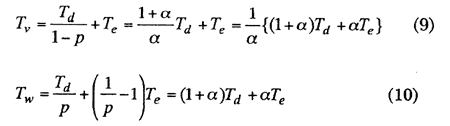
Therefore, the above two equations have the following relation:

T_w = α T_v.

　

3.2 Evaluation due to ratio of maintenance number

For the first time, we introduce the symbol M that means the number of maintenance per unit time in the long term of system operation. Then we can obtain the following relation: that is,

M = M_v M_w

where M_v + and M_w are the number per unit time of CM and PM respectively. Therefore, form eqs. (9) and (10),

　

　

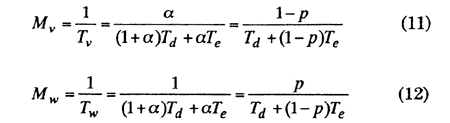
Finally, we get the following relation,

BACK　　　CONTENTS　　　NEXT