Next, let's consider the maintenance number ratio m = M/M₀, where M₀ is the maintenance number per unit time in the basic maintenance model. That is, there is no fault diagnosis, ie, p = 0 or α→∞. In other word, it corresponds to the case of CM only. Therefore, inserting p=0 into eq. (8), M₀ can be easily obtained as follows:

　

　

Finally, the ratio m is represented by

　

　

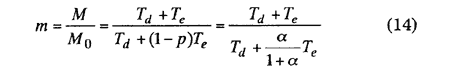
Form the above relation, the following characteristics pointed out.

1] When the diagnosis success ratio p is very close to 0, ie, α→∞, the denominator of the above equation becomes T_d + T_e and then the ratio m is 1. This result is very natural characteristic.

2] When p is near one, ie, α→0, m becomes m = 1 + T_e/T_d. From this result, the ratio m can be found to be determined by the relation of T_e and T_d.

3] Differentiating the ratio m with p, its value is always positive, and then as p increasing, the ratio m also increases monotonously and reaches to the maximum value (T_d+T_e)/T_d at p=1.

Thus, the domain of the maintenance number ratio m is as follows:

　

　

3.3 Evaluation due to reliability improvement ratio

　

Increasing fault diagnosis success ratio, the maintenance number of CM is decreasing, and then the expected interval of CM is increasing. Therefore, in order to evaluate its increasing value, the coefficient of reliability improvement k is defined as follows:

　

　

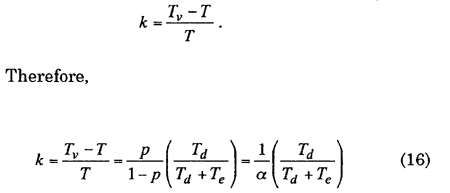
From the above equation, the following characteristics are obtained:

1] When p goes to 0, ie, α→∞, k is 0. That is, when the diagnosis fails, the coefficient k comes zero. This result shows that this case is same as the case without diagnosis.

2] When p goes to 1, ie, α→0, k becomes infinity. In this case, as the diagnosis is always success, it suggests that there might be no CM.

3] Moreover, as ∂k/∂p ＞0, k is always increasing with increase of p

　

3.4 Evaluation due to maintenance cost ratio

　

By adding the cost of CM and PM, we can represent the total maintenance cost C. First, C_v and C_w are the cost per one CM and one PM respectively. From our experiences that the former is larger than the latter, both costs are set to be

　

C_v = lC_w (l ＞ 1).

　

Thus, the total cost per maintenance can be easily obtained as:

BACK　　　CONTENTS　　　NEXT