This solution procedure is however extremely fast utilizing the monotone properties of the internal energy function.
In modeling diesel engine systems this version of pseudo bond graph model for thermo-fluid systems is regarded advantageous, because the fuel factor is so central in describing the engine processes.
In the following sections a selection of submodels for the diesel engine modeling are presented using this method of representation. Some of the models are based on the work in [12].
4.2 The cylinder model
Assuming uniform pressure, temperature and composition of the gas in the cylinder, the cylinder volume can be modeled as a single variable volume gas accumulator as described in section 3.1. Using the pseudo bond graph concept this can be represented as in Fig. 4.
Conservation of total mass, mass of burnt fuel and internal energy are expressed in the junction structure (zeros) of the bond braph. The C-field represents the accumulation of mass, mass burnt fuel and internal energy in the cylinder, and the inflow and outflow through the air- and exhaust valves is also added to the junction structure. The additional Sf element added to the thermal bond represents the work performed by the working medium on the piston and have to be added due to the use of pseudo bond graphs. The combustion process is modeled as a mass and heat source and is indicated at the top of the Fig. 4. Also included in the figure is the heat transfer model shown as a R-element added to the thermal bond. Several heat transfer models is supplied based on the works in [13] and [14].
Fig. 4. Pseudo bond graph model of diesel engine cylinder
The state equations for the cylinder model can be derived directly from the bond graph in Fig. 4 as
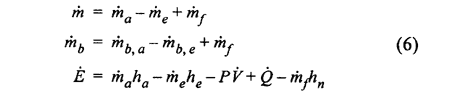
and the constitutive laws for the C-element can be derived as shown in section 3 . 1.
In the following subsections the main submodels of the complete cylinder model are introduced.
Combustion
A relatively successful approach to the problem of combustion simulation for transient performance simulations, has been to model the combustion as a heat release process, as originally proposed by Lyn [1 5]. The rate of heat release can be defined as the rate at which the chemical energy in the fuel is release by combustion.
The combustion can be characterized by the four stages ignition delay, pre-mixed combustion period, mixing controlled combustion period and the late combustion period.
The ignition delay is mainly influenced by the temperature and pressure development in the cylinder after the fuel is injected. Ignition delay data from fundamental experiments in combustion bombs have normally been correlated by equations of the form

where a and n are constants dependent on the injection process and the fuel characteristics, and E is the apparent activation energy for the auto ignition of the specific fuel. Although more complicated empirical formulas has been introduced [16], we propose to use a formula similar to Eq. (7) to evaluate the ignition delay. Default values for the constants for a medium speed diesel engine are supplied for the model.
To describe the heat release process we have selected to supply several methods. One method to be described is based on rate of heat release diagrams obtained from a specific engine at different speeds and mean indicated pressures. These results are implemented as a set of tables describing the experimentally obtained heat release. Interpolation is then utilized to calculate the heat release at other speeds and indicated pressures.
Another option for describing the heat release is to use one or two Wiebe-functions as in [17]. The instantaneous heat release using a single Wiebe-function can be expressed as
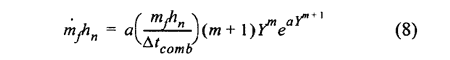
where a and m are shape constants. Y is the relative time from combustion start, mf are the total mass of fuel to be injected and hn is the absolute fuel enthalpy. In order to quantify the amount of fuel burnt in each phase, a phase proportionality factor β is introduced. Consequently the heat release for a two-phase function is described by