そこで、河川工学で用いられている洪水流の理論を用いて甲板水位の推定を行うこととした。図5.2に示すような船体固定座標系を考え、船首をx=0とし、船尾方向に向かってx軸を正にとると、甲板水位分布φ₁(x,t)は

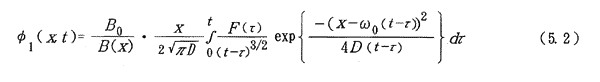
となる。ここで、D=ν₀f'/2i₀,ω₀=5ν₀/3である。f'はBow Top Height、V₀は船速を表す。F(t)を、F(t)=f(t)-f'としてf(t)は船首相対水位の時系列、i₀は縦揺れの最大角θ_max(船首上げ)を用いてsinθ_maxを表す。また、B(x)は各位置での船幅、B₀は打ち込みの有効幅を表わす。有効幅B₀は計測された一出会周期当たりの甲板水量をもとに船首相対水位の最大値がBow heightを超えた高さδに比例するとして、B₀=αδとしている。αは比例係数を表し、本部会で行った実験結果からタンカーでは1.1貨物船についてはType1、Type2及びType3(第4章参照)でそれぞれ1.05、1.1及び0.9となった。実験結果にもとづき、船首相対水位がピークに達した時間をt=0とした。

　

5.4　推定法の評価及び考察

開発した手法により推定した甲板荷重及び甲板水圧について実験結果との比較を行ったので、結果の一例を以下に示す。図5.3に正面向波(χ=180°)で波高波長比及び船速を変えた場合の甲板荷重及び甲板水圧の推定値と実験値を示す。縦軸は実船スケールに換算した値である。また、甲板荷重は甲板面積で割った値(平均水圧)を表す。これらの図から、推定値は概ね実験値とよく一致していることがわかる。波高波長比や船速が大きい場合には、甲板荷重は実験値との差が大きくなるが、これは、前述したとおり舷側からの水の流入によるものである。なお、今回示した計算例は、モデル化自体の妥当性を検証するために、入力データである船首相対水位、縦揺れ角及び船首上下速度については実験での計測値を用いた。

　

5.5　まとめ

以上のことから、Strip法等で計算可能な船体運動等を用いて甲板荷重及び甲板水位を精度よく推定できることがわかった。このツールを用いることで、ある海象において甲板上に作用する甲板荷重等の推定が可能となり、安全性の評価ツールとすることができる。

　

(文責：船舶技術研究所　小川剛孝)

前ページ　　　目次へ　　　次ページ