図4・7(a)においてはm個の電池に電流が流れていない状態即ち無負荷であれば、全起電力は次のようになる｡個数をm個とすれば全起電力E=E₁+E₂+E₃+………Em、E₁=E₂=E₃………Em=Eoとすれば

全起電力E=mE₀〔V〕……(4・4)

また、図4・7(b)において抵抗負荷R〔Ω〕を接続して電流Iを流せばm個の電池の端子電圧V_t〔V〕は次のようになる。

内部抵抗の合計r=r₁+r₂+r₃+………r_m

r₁=r₂=r₃………r_m=r_oとすれば

r=mr_o〔Ω〕……(4・5)

ゆえに、

V_t=E-rI〔V〕……(4・6)

また、

IR=V_t……(4・7)であるから

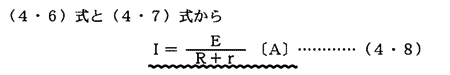
実際では電池を直列接続する場合には同一規格の同一形式のものを使用するから(4・4)式及び(4・5)式においてmE_oならびにmr_oが成り立って4・6)式のV_t及び(4・8)式のIのようになる。

　

(3)　電池の並列接続

　

電池においては規格上何ボルトで何時間率容量(船用では10時間率容量で決めてある。)というように容量は決めてある。使用にあたって容量不足であれば図4・8に示すように各電池の正極は正極同志、負極は負極同志に接続して容量を増すことができる。この接続法を並列接続という。

図4・8において、各電池の起電力をE₁、E₂、E₃、内部抵抗をr₁、r₂、r₃、抵抗負荷Rに電流を流したときの電流を〔I〕、そのときの端子電圧を〔V_t〕とすれば次のように計算できる。なお、各電池の端子電圧及び電流をそれぞれV₁、V₂、V₃及びI₁、I₂、I₃とすればV₁=E₁-I₁r₁、V₂=E₂-I₂r₂、V₃=E₃-I₃r₃となる。

　

図4・8

前ページ　　　目次へ　　　次ページ