Fig.16は5083 H112合金棒材の座屈応力-細長比曲線の一例³²⁾である。接線係数E_tは応力段階で材質によって複雑に変化するので標準化が難しく、包括的な実用式を得られ難い。以下においては、塑性域の座屈に関して、アルミニウム合金に適用されている基礎的な二、三の実験式を以下に述べる。

　

(1)　アルコア社の直線式

　

式(4)に示す直線式は、アルコア社が1938年以降の塑性座屈実験結果を集大成して1955年に公表³⁷⁾したもので、σ_k、B、D、E、f₂、f₁の各単位はpsiである。

σ_k=B-Dλ　(4)

　

　

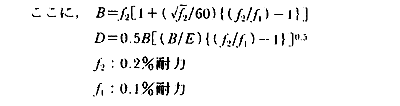
この直線がオイラー曲線と交わらない場合には、実際にf₂/f₁=1.06以上であってもf₂/f₁=1.06を用いる。f₂/f₁は、6061 T6合金が1.03〜1.036、2014 T6合金では1.031〜1.038、7075-T6合金は1.037であり、一般の構造用合金では1.02〜1.10の範囲にある。

式(4)は、AA規準に採用されている。ただし、定数B及びDは質別によって下記のように二つのグループに別けられ、部材条件と応力の種類によって圧縮耐力σ_y(最小値、Table 16及び17参照)から算定³⁰⁾できるように改良された。一様断面の柱(及び梁のフランジ)の場合は式(5)又は(6)であり、ここに、両式の単位はN/mm²、定数Cは限界細長比である。

　

　

直線式は、細長比が小さい範囲では実験結果と合致するといわれているが、高圧縮耐力の材質では傾斜線のオイラー曲線への接し方が滑らかではなく、交わる付近で過大な値を与えることがある。

　

(2)　ペリーロバートソン(Perry-Robertson)の式

　

この式の特徴はオイラー曲線に滑らかに近づき、オイラー曲線の低応力範囲では計算値が幾分安全側に位置することである。実験式を式(7)に示す。

σ_k=[{f₁+(η+1)σ_εk}/2]

-〔[{f₁+(η+1)σ_k}/2]²-f₁σ_εk〕^0.5　(7)

ここに、σ_εk:式(2)によるオイラー座屈応力

η:初期たわみによる定数

質別T6の場合　η=0.0015λ

質別T4の場合　η=0.0030λ

質別Hの場合　η=0.0075λ

英国アルミニウム開発協会(ADA)におけるHE15WP、HE15W(以上は2014合金相当)、HE10WP及びHE10W合金各H形材を主とした実験結果³⁸⁾は計算式とおおよそ合致しており、直線式及び接線係数式との比較も検討された。

　

Fig.16　5083-H112合金押出棒の座屈応力-細長比曲線³²⁾

前ページ　　　目次へ　　　次ページ